アメリカを二分した「モンティ・ホール問題」をベイズ統計学で推定する

人工知能や画像解析など、最先端の技術に使われている「ベイズ統計学」を、中学数学さえ忘れても理解できるようやさしく解説した新刊『完全独習ベイズ統計学入門』。そのエッセンスを凝縮して紹介します。
第1回では、「ガン検査」結果に対する意外な解釈を紹介しました。今回は、かつてアメリカ全土を巻き込んだ有名な論争「モンティ・ホール問題」を題材に、ベイズ統計学の重要な性質を紹介しましょう。

ベイズ統計学による推定は
主観的な問題にもアプローチできる

このコーナーでは、ベイズ統計学についてあれやこれや紹介している。ベイズ統計学とは、20世紀初頭に構築されたスタンダードな統計学（ネイマン・ピアソン統計学）に駆逐されて、いったんは表舞台から姿を消したが、20世紀後半に蘇り、現在では統計の主流派を奪還しつつある統計的な推定の方法だ。

ベイズ統計学の特徴は、「主観確率」というものを主軸に据えることである。つまり、確率を客観的な数値ではなく、主観的な数値として扱う考え方である。今回は、このことが明確になる例を紹介しよう。モンティ・ホール問題とか、モンティ・ホール・パラドクスとか呼ばれるものである。

アメリカの視聴者参加テレビ番組で、次のようなゲームが行われた。参加者は3つのカーテンＡ、Ｂ、Ｃの前に立つ。3つのカーテンのどれか1つの裏に賞品の自動車が隠されている。参加者は3つのカーテンの1つを選び、そこに自動車が隠されていれば、その自動車をもらうことができる。

そこで、参加者が1つのカーテン、例えば、カーテンＡを選んだ。司会者のモンティ・ホール氏は、選ばれなかったカーテンのうちのＢを開いてみせて、「ここには自動車はありません」という。そして、「残るカーテンは、あなたの選んだＡと、私が開かなかったＣの2つです。あなたは今ならまだ、選ぶカーテンを変えることができますが、どうしますか？」と訊ねる。このとき、参加者は選んだＡのカーテンのままにすべきか、それとも、Ｃのカーテンに選び変えるべきか？

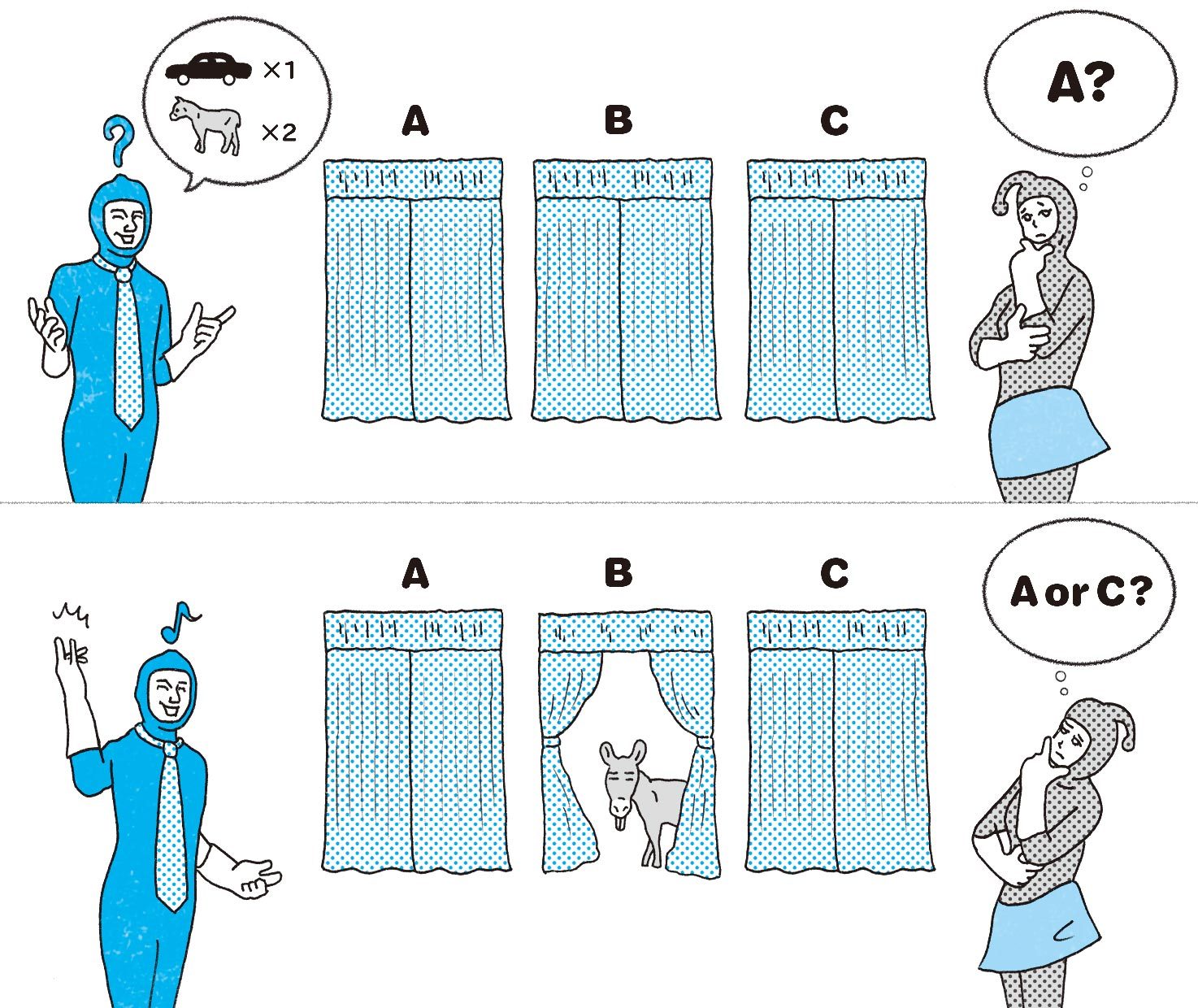この問題は、アメリカのテレビ番組「Let's make a deal!」の司会者であるモンティ・ホールさんの名前からきています。

「カーテンを選びかえる」が正解!?
多くの論争を巻き起こした意外な答え

なぜこの問題が、「パラドクス」と呼ばれるか、というと、その答えが意外だからである。この問題において「正しい」とされている解答は、「カーテンを選び変えるべき」というものだ。その理由は、「カーテンＣの裏に自動車が隠されている確率がＡのそれより大きくなるから」ということである。

具体的には、自動車が隠されている確率は、Ａのカーテンが3分の1で、Ｃのカーテンが3分の2だ。この解答を、有名なコラムニストが表明して、ひと騒動が起きた。なぜなら、多くの人は、「1つのカーテンが開けられ、自動車の隠された可能性のあるカーテンが2つになったのだから、自動車が隠されている確率は両方とも2分の1であり、どちらを選んでも確率は変わらない」と考えたからだ。

コラムニストの解答は、ベイズ統計の標準的な使い方に沿ったものである。厳密な解法は、拙著『完全独習ベイズ統計学入門』で読んでもらうとして、おおざっぱに解説すると次のようになる。最初にカーテンＡを選んだ参加者が直面している世界は、バーチャルなものが3つある。その1「Ａに自動車」、その2「Ｂに自動車」、その3「Ｃに自動車」の3つである。

その1の場合は、司会者はＢとＣのカーテンを五分五分の確率で開くと考えられる。その2なら必ずＣのカーテンを開き、その3なら必ずＢのカーテンを開く。見積もりたいのは、カーテンＢが開かれた下での世界その1と世界その3の確率である。

世界その1だった場合、カーテンＢが開かれる確率は2分の1、世界その3だった場合、カーテンＢが開かれる確率は1である。したがって、世界その3である可能性は、世界その1である可能性の2倍大きい。つまり、世界その1の直面している確率は3分の1で、世界その3に直面している確率は3分の2ということになるわけだ。ざっくりまとめれば、Bを起こしにくい状況と起こしやすい状況があるとき、Bが起きたのを観測したなら、後者の状況である可能性が高いと判断する、ということである。

「主観確率」を扱うおかげで
応用範囲が広いベイズ統計学

このモンティ・ホール問題は、多くの人の興味をそそるらしく、ネット上にもいろいろなアプローチがエントリーされている。しかし、筆者は、この問題に対する「正しい」解答というのを議論するのは無意味に思える。なぜなら、この問題への解答は、どのみち「主観」的なものにすぎないからだ。実際、ベイズ統計を使ってさえも、この解答を「ＡとＣの可能性は五分五分」と結論する設定も可能なのである。詳しくは、前掲の拙著を見てほしい。

そもそも、自動車がＡとＣのどちらのカーテンに隠されているかは、既に決定してしまっている。にもかかわらず、Ｂのカーテンが開かれたことで確率が変化するとはいったいどういうことなのだろうか。これは、客観的な意味で値が変化するのではなく、観測者の「主観の数値」が変化する、と考えるしかない。これは、ベイズ統計で扱う確率が主観確率なのと整合的である。逆に言えば、主観なのだから、どんな数値が結論されてもかまわない。問題は、その主観にどのくらいの妥当性・戦略性があるか、ということだけだ。

ベイズ統計学の面白さは、主観確率という怪しげなものを扱うおかげで、スタンダードな統計学には不可能な推定が可能になる、という点である。ベイズ統計は、主観確率によって、その柔軟性と汎用性を獲得するのである。