『大人のための中学数学勉強法』の著者・永野裕之氏によると、数学の勉強法を間違ってしまう人、つまり数学を苦手とする人の多くは、そもそも「数学」と「算数」の違いを正しく理解していないという。中学数学をめぐる本連載の前篇として、そのポイントを分かりやすく解説してもらった。
算数は結果、数学はプロセス
同じ数式を扱っているのに、中学に入ると科目名が算数から数学に変わります。しかしそのことに疑問をもつ子どもは多くありません。
「大人になった、ということかな」
とわけのわからない理由で納得(?)して、ノリは算数のままで授業に入っていきます。私はこのことが数学の勉強法を間違う人を多く生んでしまう元凶だと思っています。
繰り返しますが、数学は算数とは似て非なるものです。大胆に言ってしまうと、算数では正しい結果を得ることに価値がおかれ、数学では結果そのものよりも、どうやってその結果に達したかのプロセスに価値がおかれます。すなわち算数では計算の正確さが、数学では論理の正しさが求められているのです。
たとえば、23×15のような計算を行ないたい場合、暗算が得意でない限り、ほとんどの人が(私も含めて)下記のような筆算をしますね。
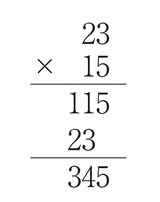
算数ではこの計算方法でなぜ正しい結果が得られるかを考えることはないと思います。小学生が「筆算を使うと正しく計算できる理由」を考えなくてはいけない場面はほとんどないでしょう。なぜなら答えが正しければそれでよいからです。23×15の計算を、算盤を習っている子どもが算盤式の暗算で答えたとしても、あるいはちょっと知識のある子がインド式で計算したとしても、正しく「345」でありさえすればちゃんと点がもらえるはずです。
しかし筆算を数学として捉え直すと、この計算方法で正しい結果が得られる理由が求められます。数学が論理の正しさに重点をおいている以上「なんでこれで正しく計算できるの?」という質問に答えられる必要があるからです。
上の質問に答えるために、まずは私たちが通常使っている10進法について確認しておきましょう。特に断りがなければ、「23」と書かれている場合それは「10が2つと1が3つ」だという意味です。そんなの当たり前だ、と思われるかもしれませんが、じつは10進法は必ずしも「当たり前」ではありません。たとえば、古くはシュメールやバビロニアでは60進法が使われていましたし、現在もナイジェリアやネパールの一部の言語では12進法が使われています。
また単位系には10進法でないものも広く使われていて、たとえば1フィート=12インチや時計は12進法ですし、1分が60秒であったり、1時間が60分であったりするのは60進法です。これらが10を基準としていないのは10より12や60のほうが、約数が多くいろいろな数で割ることができるからだと言われています……話がそれましたね。





