神はその昔、自らの姿に似せて「人類」と「使徒」を造り給うた。両者の遺伝子は本来、近いものがあったが、「生命の樹の実」を与えられなかった人類は、不完全な存在であった。そこで特務機関は科学技術を結集し、「生命の樹の実」を自らの手で作り上げ、人類の不完全性を補完する計画を推進しようとした。ところが、それを阻止すべく、「使徒」が襲来することになった──。
とまぁ、そういうストーリーのアニメDVDをレンタルしてきて、この週末に家族で鑑賞した。マニアの立場からすればレンタルなどは邪道であり、新品を2本取りそろえ、そのうちの1本を永久保存版とするのであろう。繰り返し鑑賞するのであれば、新品やレンタルではなく、中古品を入手するほうが効率的といえる。
DVDに添付されていた「新世紀エヴァンゲリオン」の挿し絵を眺めているときに、レンタルはともかくとして、中古品は新品の市場価値を支える方向に作用するのではないか、という仮説を想定してみた。今回はこの仮説を検証してみたい。
中古車市場は、
新車の販売不振を加速させるのか
新品を購入した後、それを中古品として売買するビジネスモデルが違法かどうかについては、かつて最高裁まで争われたことがあった。コトの顛末は、第28回コラム(キヤノン&リコー編)で紹介した。
概要を説明すると、インク・カートリッジの再利用に関してはメーカー(キヤノン)がリサイクル業者に勝訴したが、ゲームソフトに関してはリサイクル業者(中古ソフト販売業者)のほうが勝訴した。裁判の結果が異なった理由については、上記のコラムを参照していただきたい。
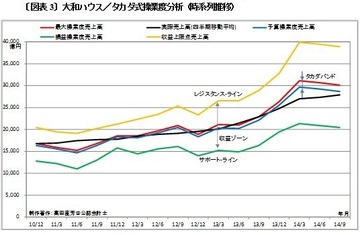
ゲームソフトやアニメソフトの新品や中古品を扱う上場企業のデータは乏しいものがあるので、新車(日産自動車)と中古車(ガリバーインターナショナル)に置き換えて話を進める。
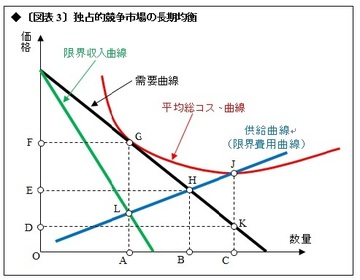
中古車を議論するにあたっては、「レモンの問題」が有名だ(「マンキュー経済学Ⅰミクロ編」655頁)。中古車の売り手は車の欠陥を知っているが、買い手はそれを知らない。売り手と買い手に「情報の非対称性」があることから、走行距離が100キロ程度であっても、中古車は格安で販売されることになる、というものだ。これを「逆選択」または「逆淘汰」という。
そこで中古車ディーラーが登場する。ディーラーは、欠陥車(これを「レモン」と呼ぶ)の有無を診断して適切な点検整備を行ない、買い手に安心感を与える役割を担うのだ。これを「シグナリング」という(前掲書656頁)。
人気車種の場合、稀に中古車の価格が新車を上回ることがあるが、中古車は総じて新車よりも安い。ましてや、中古車ディーラーが「レモンの問題」を解決してくれるのであれば、買い手が中古車市場に足を運ぶ可能性は高くなる。
筆者の住む栃木県には、ニッサンやホンダなどの下請けをしている中小メーカーが多い。中古車市場があるせいで「新車が売れない」と恨み節を漏らす企業経営者の声をときどき聞く。中古車が売れたところで、下請けには1円の収益ももたらさないからだ。