オプション理論が重要なのは、空売りやデルタヘッジといった金融市場での取引に有効だからだけではない。これは生命保険や損害保険のような「不確実性に賭ける投資」の価値を判断する上で、重要な示唆を与えてくれる。ファイナンス理論の入門書『あれか、これか』のなかから紹介していこう。

空売りを使って「無風状態」をつくる

前々回および前回に見たとおり、オプションの価値は期待リターンの大きさではなく、リスクの大きさ（ボラティリティ）で決まる。ここが株式の現物取引とオプション取引との決定的な違いである。

これについて、具体例とともに見ていくことにしよう。

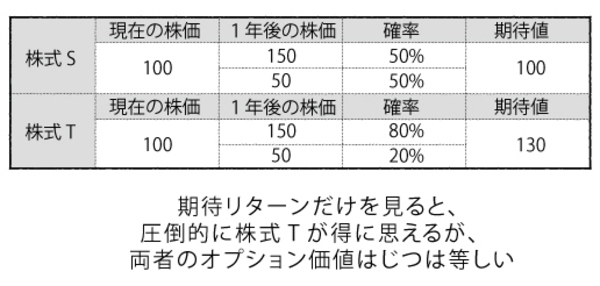
株式Ｓと株式Ｔがある。2つともいまの株価は100円だ。そして両方とも1年後には150円になっているか50円になっているかどちらかしかないとしよう。

株式Ｓは上がるか下がるかの確率が50％ずつなのに対し、株式Ｔのほうは150円に上がる確率が80％、50円に下がる確率が20％となっている。

1年後の株価の期待値は、株式Ｓは100円に対し、株式Ｔは130円（＝150円×80％＋50円×20％）となる。明らかに株式Ｔのほうが魅力的だ。

ハイリスク・ハイリターンの法則に従えば、リスクがあるのに期待利益が0円（＝1年後の期待値100円－現時点の株価100円）の株式Ｓを選ぶ人はいない。

ここまではいわば常識の領域である。問題はオプションだ。

【問題】株式Ｓ・Ｔを1年後に100円で買えるコール・オプションが売買されている。
このとき、どちらのオプションの価値が高いか？

直感的にはやはり株式Ｔのオプション料のほうが価値が高そうだ。しかし、ファイナンス理論では、そうはならない。ＳとＴのオプション価値は同じである。オプション価格は、期待リターンの大きさではなく、リスクの大きさで決まるからだ。