本日は衆議院議員選挙の投票日。民意を反映させるはずの選挙が、実は日本の政治をいびつにゆがめているとしたらどうだろう。多数決や選挙といった「決め方」の意味を経済学的に鮮やかに解説した名著『「決め方」の経済学――「みんなの意見のまとめ方」を科学する』の著者である坂井豊貴氏によれば、多数決が持つ「票の割れ」という性質が、政党政治のあり方に強く影響を与えているという。2016年刊の同書より、ぜひいまこそ読んでほしい一節を紹介する。
(『「決め方」の経済学』より一部を特別に公開しています。 初出:2016年7月8日)
選択機会が豊かだと
多数決の結果は歪む
 Photo: Adobe Stock
Photo: Adobe Stock
「決め方」は決定的に重要である。それしだいで結果はまるで変わる。
いま、「ネーダー・ゴア・ブッシュの順に支持する有権者」を考えてみよう。選挙にネーダーが不在ならば、彼にとっては2位に支持するゴアが勝っていた。なのに1位に支持するネーダーが選挙に加わると、3位のブッシュが勝ってしまう。彼にとって最も好ましい候補の出現が、最も好ましくない結果を導くわけだ。
多数決の選挙だと、選択機会が豊かになることが、結果を奇妙に歪ませてしまう。では、そうならない選挙の方式には何があるのか。
一番単純なのは、多数決に決選投票を付けることだ。初回の多数決で1位が過半数の票を集めなかったら、1位と2位で決選投票を行う。ブッシュとゴアが決選投票に進み、ゴアがそこで勝利するというように。
より本格的な変更案には、「1位に3点、2位に2点、3位に1点」と順位に配点するボルダルールという決め方がある。ボルダルールのもとだと、多数いるゴア支持者はゴアを1位にして、またネーダー支持者はゴアを2位にするだろうから、ゴアの総得点はほかの候補と比べて最大になり勝利したはずだ。
この大統領選だと、決選投票でも、ボルダルールでも、どちらでもゴアが勝つと考えるのが妥当だろう。
「決め方」次第で
結果は変わる
ただし一般には、両者は異なる選択肢を勝たせる。簡単な例として、有権者が9人で、選択肢はABCの3つがある図表1-2の例を考えてみよう。この図表の読み方だが、例えば4人の有権者は上からACBの順序で支持する、と読む。有権者は選挙でこの順序にもとづき投票すると考える。
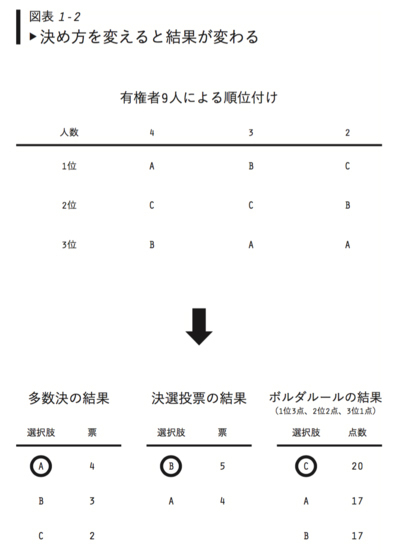
多数決だとどの選択肢が勝つか。有権者は自分の「1位」に投票する。4人がA、3人がB、2人がCに投票するので、勝つのはAだ。
しかし決選投票の付いた多数決だとそうはならない。初回の多数決で最多の4票を集めたAと、次点で3票を集めたBが決選投票に進んで、そこではBが勝つ。
なぜなら決選投票では、もとからBを支持していた3人に加えて、もともとはCを支持していた2人がBの支持にまわるので、計5票がBに入るからだ。一方のAは決選投票でも4票のままなので、計5票のBに負けてしまう。
ではボルダルールだとどうなるのか。結論からいうとCが勝つ。得点を計算してみると、AとBは17点で、Cは20点だからだ。計算例としてBの得点を求めてみると、17点=(3点×3人)+(2点×2人)+(1点×4人)である。
多数決ならA、決選投票付き多数決ならB、ボルダルールならCが勝つ。決め方しだいで結果はさま変わりだ。では、どの決め方が、いかなる意味でよいのだろう。この問いは『「決め方」の経済学』で詳しく考えていくとして、ここでは決選投票付きもボルダルールもAを選ばない、という点を強調しておこう。
Aはの多数決だと勝つけれど、実はAはとても「少数派」な選択肢だ。どういうことかというと、二択のAとBで多数決をしたらBが5対4で勝つし、AとCで多数決をしてもCが5対4で勝つ。なぜならAは、BやCを支持する過半数メンバー5人(=3人+2人)にとって、最下位の選択肢だからだ。
このように、ほかのあらゆる選択肢にペアごとの多数決で全敗する選択肢のことをペア敗者という。決選投票付き多数決も、ボルダルールも、ともにペア敗者であるAを選ばない。



