エイリアンがいる星の数、ざっくり概算した結果とは？

「フェルミ推定」は、調べても正確な答えがわからないような一見難解な問題だ。
でも、地頭のいい人はわずかな手がかりだけでパッと概算することができる！
本連載では、ビジネスでも日常のひとコマでも使える超・高速計算テクニックと、どんな難問でも自分なりの答えを導くコツを紹介したイギリスで話題の1冊、『世界の猫はざっくり何匹？　頭のいい計算力が身につく「フェルミ推定」超入門』より一部を特別に公開する。

エイリアンはどこにいる？

　エンリコ・フェルミは、封筒の裏で問題を解く一般的な方法とは別に、ある特別な計算でも歴史に名を残している。

　第二次世界大戦が終わってから間もない頃、フェルミが何人かの科学者とおしゃべりをしていると、地球外生命体の話題になった。するとフェルミは突然、「でも連中はどこにいるっていうんだい？」と問いかけたという。銀河系には数十億の星があって、そのうちの1つは明らかに高度な生命体を生み出したはずなのに、どうして地球はまだエイリアンに侵略されていないのか、というのだ。

　この疑問は、「フェルミのパラドックス」と呼ばれるようになった。

　それから何年か経ち、宇宙物理学者のフランク・ドレイクが、通信をする知的文明が銀河系の中に現在いくつ存在するか（N）を表した方程式を考えついた。その方程式とは、次のようなものである。

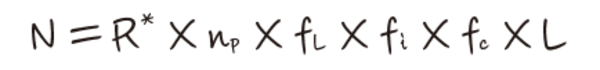
・R*は、1年間に生まれる恒星の平均個数
・npは、1個の恒星が持っている惑星の平均個数
・fLは、それらの惑星のうち生命を発生させるものの割合
・fiは、その中で知的生命に進化する割合
・fcは、その中で通信技術を発達させる文明が生まれる割合
・Lは、通信をする文明が存続する年数

　複雑そうに見えるけれど、実は常識を数式に落とし込んだだけだ。難しいのはそれぞれの係数に数値を当てはめるところで、それは概算するしかない。

　たとえば、ある特定の恒星のまわりに形成される惑星のうち、生命を発生させられるものの割合は？ 試しに理にかなった数値を考えようとするだけでも、生命体の存在に欠かせない化学的・物理的環境に関する知識が必要だ。

　これまでにさまざまな科学者が、それぞれの係数にもっともらしい数値を当てはめようとしてきた。

　1年間に生まれる恒星の平均個数については、1から10まで幅がある。生命を生み出せる惑星の、恒星1個あたりの個数は、0.2～2.5の範囲、そのうち知的生命が生まれる惑星の割合は1～10％、そのうち通信技術を発達させるのは1～100％と推測されている。通信をする文明の存続期間については、科学者によって100年から10億年までまちまちだ（ある科学者は304年という数値をはじき出しているが、これほど細かい数だとむしろ怪しい）。

　それぞれの係数について中くらいの数値を選ぶと、次のようになる。

3×0.5×5％×30％×1000はジコールで10（ジコールについては本連載の第三回『イギリスで話題の数学者が伝授！ 誰でも超高速で計算できるワザとは？』をご覧ください）

　つまり、通信ができて、そのため僕たちが見つけられるかもしれない文明は、地球外に10個はあるのかもしれない。

　でもこの個数は、方程式に放り込む数値にとてつもなく敏感に左右される。現在、銀河系内で通信をしている文明の個数の推定値は、1×10のマイナス10乗（つまり事実上0）個から1500万個まで幅がある。封筒の裏での問題の答えとして、これまでに出された中でも一番ばらつきが大きいに違いない。

　このドレイク方程式は頭の体操としては楽しいが、このくらいでやめておこう。せっかく概算をしても役に立たないことがあるんだって、よく分かったはずだ。

（本原稿は『世界の猫はざっくり何匹？　頭のいい計算力が身につく「フェルミ推定」超入門』ロブ・イースタウェイ著、水谷淳訳の抜粋です）