統計学の解説書ながら42万部超えの異例のロングセラーとなっている『統計学が最強の学問である』。そのメッセージと知見の重要性は、統計学に支えられるAIが広く使われるようになった今、さらに増しています。そしてこのたび、ついに同書をベースにした『マンガ 統計学が最強の学問である』が発売されました。本連載は、その刊行を記念して『統計学が最強の学問である』の本文を公開するものです。第27回では、データの中から有益な情報を得る手法やプロセスである「データマイニング」について解説します。（本記事は2013年に発行された『統計学が最強の学問である』を一部改変し公開しています。）
Photo: Adobe Stock
統計学がITとの融合によってその影響力を爆発的に拡大させた、というのはすでに述べたところだが、その結果として生じたのがデータマイニングと呼ばれる研究領域との接触である。
統計家が手計算の代替としてITを利用するようになったという歴史とは対照的に、データマイニングの技術はITの進歩によって生みだされたものである。そのためなのか、IT分野においては「データマイニング」という単語は、「統計学」という言葉よりもずっとよく知られている。私自身「新しい分析用データベースを導入したんだけど、どうにかデータマイニングできない？」といった相談は受けても、「どうにか統計解析できない？」という相談をもらったことはない。
その一方、実際にどのような課題や目的があるのかよく話を聞いてみると、「データマイニング的な手法」よりも、統計学的な手法こそが真に必要だった、ということもしばしばである。
「回帰分析」という古臭い統計学の教科書に書かれてあった漢字の言葉よりも、「ニューラルネットワーク」という横文字のほうが何だかかかっこいい、という気持ちはわかる。また「人工知能の領域で研究されてきた、人間のニューロンをシミュレーションしたものなんです」と説明されれば、何かものすごい技術だという気もしてくる。
だがデータマイニングと統計学の考え方や手法について、どこが違って、どこが共通しているのかがわかれば、今自分に必要な手法はどちらなのかきちんと考えることができるだろう。次はそのあたりについてお話したい。
意外なほど新しいデータマイニングの歴史
じつはデータマイニングという分野の起こりがどこにあるか、という話はたいへんむずかしい質問である。「データマイニング」という言葉自体、1995年にKDD（Knowledge Discovery in Database）の国際会議で、「有用でかつ既知でない知識をデータから抽出する自明でない一連の手続き」と採択されるまでは、いろいろな人がいろいろな文脈で使っていたらしい。
フィッシャーが「生物統計学の父」であるように、広く「データマイニングの父」と認識されているような人は存在していないようだ。
その理由は、データマイニングが学者の手によるものという以上に、マーケティングやデータ処理の「現場」で生まれたものといえるからである。かつてデータマイニングを行なっていた者には、統計学的素養などまったくないという人もいた。
だが統計家が紙の上で数式を弄んだり、自分で集めた学生に対するアンケート結果や実験動物の検査値を手計算したりしていた時代から、すでに彼らは実際のデータを大量に持っていたし、ここから役立つ情報を引き出す必要があった。バーコードの規格が整理され、スーパーマーケットでPOSシステムの普及が始まったのは1970年代の話だし、データベース界の王者であるオラクル社が創業したのも1970年代の終わりである。
一方で、この時代は統計家であっても「コンピュータを触る」という行為がそれほど一般的なものではなかった。私より20～30年ほど年上の教員によると、彼らの学生時代は「ごく簡単な統計解析を行なうプログラムを書いただけで卒論になった」らしい。
「おむつとビール」でバスケット分析
そんなわけでデータマイニングの黎明期には、データに触れるITの技術者や現場のマーケターたちによってさまざまな応用が行なわれるようになった。
中でも有名なものは、1993年にIBMの技術者ラケシュ・アグラワルが英国の百貨店マークス＆スペンサーのために作ったバスケット分析と呼ばれる手法だろう。データマイニングに関心のある人なら「おむつとビール」という事例として聞いたことがある人もいるかもしれない。
たとえば1000人分の「バスケット」つまりスーパーマーケットの会計について、「おむつを買ったかどうか」と「ビールを買ったかどうか」で集計を行なったところ、図表40のような結果が得られたとしよう。ビールとおむつを同時に会計した人は20人、ビールだけを買った人は280人、おむつだけを買った人は30人おり、どちらも買っていない人が670人という内訳だ。
こうしたデータから何がわかるか、とアグラワルは問われ、おそらくはまず「おむつを買った人のうち40％（50人中20人）がビールを購入しています」という部分に注目した。ビール以外の商品と比較しても「おむつを買っている人」がおむつと同時に買っている可能性が一番高いのはビールだ。だったらおむつを買っている人にビールをオススメすれば売上は伸びるのではないだろうか、というのだ。バスケット分析において、こうした「ある商品を買っている人が別の商品を買っている割合」は信頼度（Confidence）と名付けられている。
「確かにそうだ」と思った人は少し待ってほしい。もともとおむつを買う人と比べ、ビールを買う人は多い。人間がおむつをしている期間はせいぜい2～3年だが、成人男性の多くはビールを飲む。もし仮に、本来なら半数以上のバスケットの中にビールが含まれているはずなのに、おむつを買っている若い父親が飲酒を自粛し、ビールの購買率が40％に留まっていたとすれば、ビールのオススメに意味はない。
だからバスケット分析では改善度（Lift）と呼ばれる指標も用いる。つまりおむつを買う買わないを限定しない全顧客中のビール購買率（1000人中300人で30％）と比べて、おむつ購買者に限定したビールの購買率（50人中20人で40％）はいったい何倍になっているか、というのがこの改善度にあたる。今回の例で言えば1.33という値がおむつ購買によるビール購買の改善度となる。これがたとえば1以上であれば、何かしらの改善が見られるということであるというのがバスケット分析の考え方だ。
だが、これでもまだ不十分であるのは図表41の事例を考えてみればわかると思う。
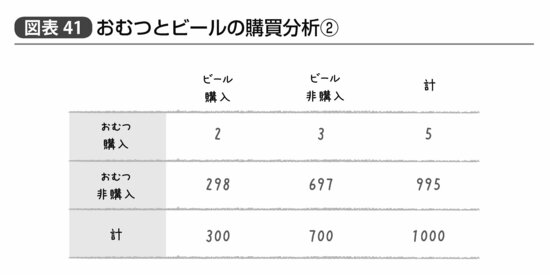
先ほどと同じくおむつ購買者の40％（5人中2人）がビールを購買しているから信頼度は0.40だ。またおむつを買う買わないを限定しない全顧客中のビール購買者も変わっていないから改善度も同様に1.33だ。
だが、もしおむつとビールを同時に買った2人のうちどちらかが、たまたま気まぐれにビールを買わなかったとしよう。そうすると信頼度は0.20と半減するし、改善度も0.67と「むしろ改悪」という結果になってしまう。それに、そもそもおむつを買っている人がごく少人数しかいないのであれば、「ビールを買いやすい」という予測ができたとしてもあまり売上を増やす役には立たない。
だからバスケット分析では「あまりに数の少ない組み合わせについては考えないことにしよう」と、「ビールとおむつを同時に買っている人」が全体の中でどれだけいるかを用いる。この値を支持度（Support）と呼ぶ。図表40では支持度が0.02（1000人中20人）、図表41では0.002（1000人中2人）で区別ができるというわけである。
バスケット分析よりもカイ二乗検定を
こうしたシンプルな計算だけで何かしら関連性のある商品を見つけられる、というのがバスケット分析の利点であるが、統計学を知っていれば「もっとよいやり方があるではないか」とすぐに気づく。Googleの共同設立者であるサーゲイ・ブリンもその1人であり、彼は学生時代に「バスケット分析より統計学的な相関分析のほうがいい」という論文をわざわざ発表している。
こうした集計表の相関を分析するとき、統計学ではカイ二乗検定の計算のもととなっているカイ二乗値を用いる。カイ二乗検定が一般化線形モデルの中で説明できることはすでにみなさんご存じのはずだ。カイ二乗値を使えばフィッシャーの言う「推定値の誤差」のようなものを考慮することができるため、支持度のような指標を用いることもなく、カイ二乗値が大きければそれは自動的に改善度だって大きいのである。なお、それぞれの商品の販売有無という二値変数間で、カイ二乗値の大きい組み合せを選ぶことと相関係数の絶対値が大きいものを選ぶことは、まったく同じ意味を持っている。
バスケット分析では改善度や支持度を見ながらあれやこれやと検討しなければいけなかったが、カイ二乗値を使ったものであれば誤差に騙されることなく自動的に関連性の強い商品の組み合わせを探すことができる。なおAmazonの商品のレコメンドでも、こうした相関分析が行なわれている。
▶『マンガ 統計学が最強の学問である』の刊行に寄せて
『マンガ統計学が最強の学問である』は、言語化・定型化された仕事がAIに奪われていくなかで、「新たに何をするか考えて決める」スキルを日本に最大限広げるために制作されました。
実は初代『統計学が最強の学問である』はほとんど数式を使わず、統計学がどう生まれてどう役に立てられるのかにフォーカスした、統計学の本としては少し変わった本でした。しかし、40万部以上売れただけあって、あの本を読んで統計学を面白いと感じ、本格的に勉強しようとしたり、実務に活かすようになった、という方と私は日々の仕事の場で頻繁にお会いします。統計手法の数理面を細かく説明したり、統計解析をおこなうためのプログラミングに関する本は多数ありますが、それはちょうどAIのサポートが手厚くなっている部分です。今の時代はそれよりも、「統計学を活用したい」というモチベーション、「どのような課題に対して統計学を活用するか」という課題設定のコツ、そして分析結果の読み解き方と、結果を踏まえて何をやるべきかを考える枠組みといったスキルのほうが相対的に重要になってきているのではないでしょうか。
本書が目指すのは、まさにそうした今こそ必要な「統計学の活かし方」を、物語を通して皆さんにお伝えすることです。たとえば『SLAM DUNK』というマンガを読むことでバスケットボールをプレイするモチベーションが喚起されたり、バスケットボールの観方がわかるようになったりといった方がたくさんいるように、すばらしいマンガは多くの人の人生を変える力を持っています。ありがたいことに私にとっても大好きな漫画家であるうめさん（小沢高広さんと妹尾朝子さん）に漫画制作を依頼できたことで、ストーリー面でも作画面でもすばらしいものになりました。私自身のデータ活用に関わる経験を凝縮した物語を、うまく追体験していただければ幸いです。
また各話の最後には、それまでに出てきた統計手法について、できる限りわかりやすく、かつ簡潔に説明した解説を加えました。ストーリー内ではあまり説明臭くならないよう、しかし気になるであろう知識面はその後の解説で補足できるよう個人的にバランスをとったつもりです。
本書をきっかけに、さらに多くの人が統計学を学び、「新たに何をするか考えて決める仕事」をする力を手にしていただければ幸いです。
