統計学の理解が劇的に進む「1枚の表」とは？

統計学の解説書ながら42万部超えの異例のロングセラーとなっている『統計学が最強の学問である』。そのメッセージと知見の重要性は、統計学に支えられるAIが広く使われるようになった今、さらに増しています。そしてこのたび、ついに同書をベースにした『マンガ 統計学が最強の学問である』が発売されました。本連載は、その刊行を記念して『統計学が最強の学問である』の本文を公開するものです。第21回では、初出時に大きな話題を呼んだ、統計学の理解が劇的に進む「1枚の表」を紹介します。（本記事は2013年に発行された『統計学が最強の学問である』を一部改変し公開しています。）

統計学の教科書は一般化線形モデルの扱いで2種類に分けられる

　回帰分析はそれ自体有用なツールでもあるが、そこから多くの統計学的手法を「広義の回帰分析」として統一的に理解すれば、さらにその応用範囲は広がるだろう。

　このような「広義の回帰分析」という考え方は、統計学者たちから一般化線形モデルという名で呼ばれている。線形とは回帰分析のように直線的な関係性のことを指し、「いろいろ手法はあるけど結局回帰分析みたいなことしてるっていう点で、一般化して整理できるよね？」というのが一般化線形モデルの意図するところだ。

　極端な表現をすれば、基礎統計学の教科書は大きく2つに分けられると私は考えている。一方は一般化線形モデルという視点を活かさないためにフィッシャーたちの時代に作られた手法を「別々のもの」として紹介している本、そしてもう一方は「基本的に同じ手法」として俯瞰した形で説明している本である。

　前者の書き方でしばしば起こる悲劇は以下のようなものだ。

　t検定だとか回帰分析だとか、呼び名の由来がわかるわけでも規則性があるわけでもない個別の手法をいちいち覚え、結局のところどういうときに何を使えばよいのか、という点についてはわからずじまい。何となく演習問題で解かされた手計算のテストで単位はもらえたが、結局あれはいったい何だったのだろう、と大人になってから統計学について思い返すたびに首をひねることになる――。

　これが「基本的に同じ手法」というコンセプトのもと、たった1枚の表でどう使い分けるか、何を見ればよいのか整理できたとすればどうだろうか？ 統計学の理解のために必要な手間は劇的に減少し、ずいぶん見通しがよくなると思う。

　そのたった1枚の表とは図表25のようなものだ。

　本書では統計学の目的として、フェアな比較に基づき違いを生む要因を見つけることを何度もあげているが、どのような分析軸で（これを説明変数と呼ぶ）、どのような値を比較したいか（こちらは結果変数と呼ぶ）、ということさえ決まれば、用いるべき手法は簡単に選べる。繰り返すが、この表に載せられたものはすべて同じ「一般化線形モデル」という広義の回帰分析なのである。

「1枚の表」の使い方

　たとえば、顧客の1人当たりの売上という変数は0円から1円刻みで増加する連続値である。これを結果変数として、2グループ間（たとえば男女別の違いなど）での比較を行なう際にはそれぞれの平均値を記述し、t検定によって得られた「この平均値の差は誤差の範囲と言えるかどうか」というp値や信頼区間を示せばいい。

　また、来店回数という値も連続値であるが、「来店回数が多い人ほど売上も高まるのだろうか」という比較を行ないたければ、来店回数を説明変数、売上金額を結果変数とする回帰分析を行ない、回帰係数の推定値や信頼区間、p値を示せばいい。

　同様に金額に関係なく、「購買の有無」や「来店の有無」といった値は、たった2つの値、すなわち「あり」か「なし」かで表すことができるため二値である。このような結果変数を2グループ間あるいは3つ以上の多グループ間（たとえば10歳刻みの年代カテゴリーなど）で比較したければ、集計表でそれぞれのグループの購買割合や来店割合などを記述したうえで、カイ二乗検定により「誤差の範囲と言えるかどうか」を示すp値を示せばよい。

　少しややこしいのは、連続値でもなく二値でもない、つまり「何カテゴリーかに分類される」という結果変数を扱うにはどうすればいいかという話だが、これも実用上は二値もしくは連続値として扱うことが多い。

　たとえば「1．まったくない」「2．あまりない」「3．たまにある」「4．よくある」といったようなアンケート項目には1→2→3→4というような順位や方向性が存在している。こうしたカテゴリーについては1～2か、それとも3～4か、といったように二分することで二値の変数として扱うというのが1つの手だ。なお別に中央で区切らなくても、「よくある」と「それ以外」というような分類で二値にしてもまったくかまわない。また、1～4の値をそのまま連続値の数値として分析してやる、ということも実用上はしばしば行なわれる。

　一方、日本人の支持政党などというカテゴリーについては、このようなアンケート結果ほど明確な順序性や方向性を持っているわけではない。

「リベラルさ」といった尺度で直感的に並べることぐらいはできるかもしれないが、政策の領域によってその順序は入れ替わるし、別に日本人は支持政党を「リベラルさ」だけで決めているわけでもないだろう。そのため、こうした変数については「質的に異なるカテゴリー」と考え、「自民党を支持するか否か」「民主党を支持するか否か」と、それぞれの政党の支持の有無という二値の変数に変換したうえで解析することが一般的である。

　3カテゴリー以上の変数に対しては少しややこしいかもしれないが、それでもこのたった1枚の表だけでほとんどのデータの関連性を分析したり、将来の結果を予測できたりするという、とてもシンプルかつパワフルな枠組みである。

どの方法でも同じp値が得られるわけ

　さらに言えば、一番右の「複数の説明変数で同時に比較」したいときに使う手法を、1つの説明変数しかない場合に使ってもかまわないし、その場合説明変数がグループ間の比較だろうが、連続値の多寡だろうがまったく問題がない。つまりt検定をすべき場面で重回帰分析を行なおうとしても（ただしこの場合分析軸が1つしかないため重回帰分析とは呼ばれず回帰分析と呼ばれることになるが）、カイ二乗検定を行なうべき場面でロジスティック回帰をしてもまったく同じp値が得られるのである。だから関連性を分析する手法のほとんどが広義の回帰分析であると言えるのだ。

　これらの結果が一致することは本来数学的な証明によって述べるべき事実だが、t検定と回帰分析の結果が一致するイメージぐらいなら数式を使わなくても伝えることはできる。

　図表26は、t検定すなわち2グループ間の平均値の差が果たして誤差の範囲と言えるかどうかのp値を算出するための統計手法の考え方を示したものである。例として、広告認知が「あったグループ」と「なかったグループ」の間で、購買金額の平均値に違いがあったかどうかを分析するという想定で図中のデータを作成した。

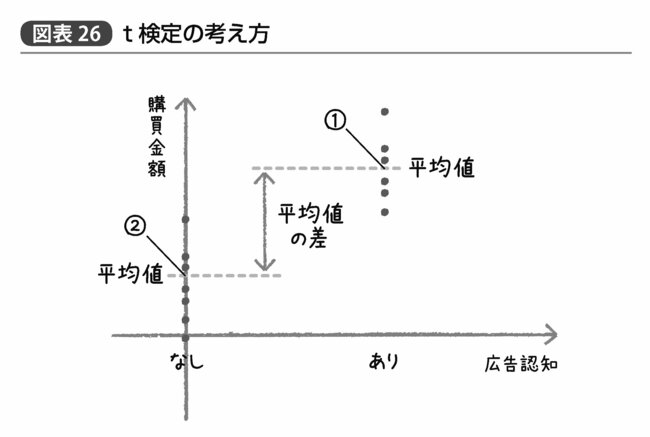
　それぞれ黒い点が各グループに分類される顧客の購買金額を示しており、①②で示したのがそれぞれのグループの平均値である。t検定で分析したい平均値とはこの①②の「高さ」の違いであり、もしこれがデータのバラつきによる誤差の範囲を越えていると考えられるならば、この広告は効果があると考えていいかもしれない。

　では、このようなデータに対して回帰分析を行なった場合、どのようなことになるのだろうか？ 図表27がその結果を示すものである。回帰分析を行なうためには両者ともに「数字」でなければならない。だから便宜的に「広告認知なし」を0、「広告認知あり」を1とすることにしておこう。

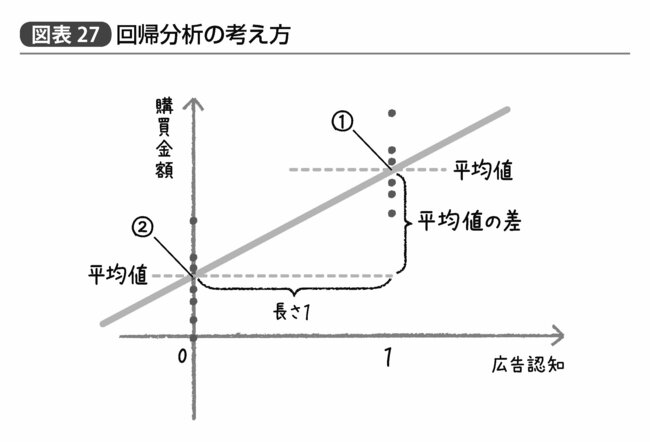
　以前も述べたように回帰直線とは「データの中心を通るもの」だ。だから当然両グループの平均値を通る直線が得られることになるのはいいだろう。そしてここから得られる傾きだが、中学校で習うようにグラフにおける直線の傾きとは「座標の縦に進む長さ÷座標の横に進む長さ」で示される。

　つまり、それぞれのグループの平均値間でこの回帰直線の傾きを考えると、「座標の縦に進む長さ」とはそのまま両グループ間の「平均値①②の差」である。そして「座標の横に進む長さ」とは言うまでもなく、1マイナス0で1である。「平均値の差」÷1は当然そのまま「平均値の差」なわけで、このようにグループ間の違いを0か1かで表現しさえすれば「平均値の差」と「回帰係数」はまったく同じ値になるのである。

　このように本来数値というわけではない「2つのグループ」あるいは「二値の変数」を、0か1かで表現するやり方のことをダミー変数と呼び、多くの論文でよく使われている。回帰分析の表に「男性ダミー」とか「高齢者ダミー」と書いてあれば、それはすなわち「男性なら1・女性なら0」とか「高齢者なら1・未満なら0」といった変数を回帰分析に使ったということである。もしその男性ダミーの回帰係数が5.2であると書いてあれば、「女性に比べて男性は5.2だけ結果変数が大きい傾向」となるし、マイナス4.1と書いてあれば「女性に比べて男性は4.1だけ結果変数が小さい傾向」と読み取ればいい。

　鋭い読者なら、「平均値の差」と「回帰係数」が一致するだけではなく、その誤差やバラつきについても考慮しなければダメだろう、という指摘をしてくれるかもしれないが、こちらについてもまったく問題はない。

　なぜなら得られたデータから算出されたグループ間の平均値も、回帰係数も、まったく同じt分布に従うバラつきを持つことがフィッシャーによって証明されているからだ。同じデータから本質的に同じ値（平均値の差と回帰係数）を推定し、しかもその理論上のバラつきが同じとくれば、結果がまったく同じになるのも当たり前である。

　今回だけで、基礎統計学の教科書1冊分の手法を説明することができたのも、一般化線形モデルという素晴らしい枠組みがあってのことである。

　このように学習者にとってわかりやすいコンセプトがネルダーとウェダーバーンによって提唱されてからもう40年ほど経つが、未だに一般的な教科書の記述に活かされていない、というのは個人的に残念である。

　以前、ハーバードの大学院生と私的な統計学の勉強会を催した際にこのような枠組みの話をすると、「なんで今まで誰もこんな風に教えてくれなかったの？」というリアクションをいただいたこともあるので、我が国の統計教育だけの問題というわけでもなさそうだ。

　ネルダーたちがそもそも一般化線形モデルというアイディアを形にできたのは、当時発明されていたさまざまな回帰という名の手法が同じ計算で実行できるのではないか？ という思いつきからスタートしている。そのため重回帰とロジスティック回帰がどう同じでどう違うか、ということさえわかれば、今後何か別の回帰分析手法を目にするときにも恐れることなくその意味を受け止められるはずだ。