統計学の解説書ながら42万部超えの異例のロングセラーとなっている『統計学が最強の学問である』。そのメッセージと知見の重要性は、統計学に支えられるAIが広く使われるようになった今、さらに増しています。そしてこのたび、ついに同書をベースにした『マンガ 統計学が最強の学問である』が発売されました。本連載は、その刊行を記念して『統計学が最強の学問である』の本文を公開するものです。第28回ではAI研究から生まれたデータマイニング手法について解説します。（本記事は2013年に発行された『統計学が最強の学問である』を一部改変し公開しています。）
Photo: Adobe Stock
人工知能の研究から生まれた高度な手法
もちろんバスケット分析のような単純な計算方法だけでなく、高度なアルゴリズムがデータマイニングで用いられることもある。ニューラルネットワークだとか、サポートベクターマシンだとか、クラスター分析だとかいう手法について耳にしたことのある人もいるだろう。
こうした手法の多くは、人工知能分野で応用されていたものである。人工知能はコンピュータサイエンスの中で長年花形分野であり、IT関係の仕事をする技術者たちが学生時代に習っていたことからよく用いられるようになったのかもしれない。
人工知能の分野の中にもいくつか考え方の違うグループが存在しているのだが、データマイニングでよく用いられている手法は人間の認知機能を「分類」というところに帰着させるグループにより生み出された。
たとえば我々人間は、適度な高さを持った家具を、どんな形だろうがうまく「椅子」であると認知する。一方、コンピュータは何が椅子で何が椅子でないかを自分で判断することはできない。このような認知をすなわち「椅子」と「椅子以外の家具」の分類であると考えるのである。
人工知能の手法において「分類」は大きく2つに分けられる。一方は「教師なし分類」であり、もう一方は「教師あり分類」である。
家具の高さや重さ、何箇所で接地しているかといったデータが与えられていたとして、ここから行なうべき分類は「いかに類似性の高いグループ」に分類するかという話である。椅子同士は椅子とタンスの間よりもデータ的な類似性が高いことを利用してさまざまな家具を分類すれば、その中の1つに「椅子もしくはそれとデータ上似た家具」のグループが存在するのではないかということになる。こうした手法が教師なし分類であり、その代表的な手法としてクラスター分析がある。
実際の応用としてクラスター分析が最もよく行なわれるのは、マーケティングにおけるセグメンテーションだ。セグメンテーションとは市場あるいは顧客を類似性の高いグループに分割することを言う。セグメンテーションを行なわないマーケティングでは下手な鉄砲を数打つように、広く一般に商品を作って宣伝して売ることになる。だが顧客の価値観やメディアの利用は多様であるので、広告費や販売費がかさむ割にムダも多い。
これをもし自社の顧客セグメントを「セレブ思考な専業主婦」と「キャリア思考の総合職女性」というセグメントに絞ることができれば、それぞれに合わせて作るべき商品や広告キャンペーンを行なうことができる。顧客のデータに対してクラスター分析を行なえば、こうしたセグメントをうまく分けてやることができるのだ。
なおクラスター分析は「分類することができる」というだけなので、分類された結果に対して、それぞれがどういうグループ（クラスター）であるかは、グループごとの集計結果から人間が解釈してやらなければならない。クラスター分析はある種のマーケティング・リサーチャーが最もよく用いる手法であり、彼らの中にはしばしばわかりやすく素敵な名前をつけるところまで含めて「伝統芸」のような仕事を行なう人もいる。
だが、もし家具のデータから椅子を見つけたいのであれば、単純な類似性によるグループ分けを行なうよりも、「これは椅子ですよ」と教えてやればいい。そうすればより正確に判別してやることができるだろう。この「これは椅子ですよ」という答えを教えてやることがすなわち「教師あり」ということである。
なぜ、データマイニングの専門家は回帰モデルを「古臭い」と言うのか？
統計学で「教師あり分類」を行なおうとすれば、「椅子か：1」「椅子でないか：0」という二値の結果変数を用いたロジスティック回帰を行なうが、高度なデータマイニングの専門家たちはこうした手法のことを、「古臭い」とか「原始的」と考える者もいる。
なぜなら回帰モデルでは「説明変数は独立して結果変数に影響している（相乗効果はない）」とか、「説明変数と結果変数の関係性は直線的なものである」といった分析しかできないからだ。
椅子の重さを説明変数として椅子かどうかという結果変数を分析しようとしたとき、1kgの椅子と2kgの椅子の差だろうが、10kgと11kgの椅子の差だろうが、「椅子の重さが1kg増えるごとに椅子である確率は同じだけ下がる」というのが直線的な関係ということである。逆に、1kgから2kgに増えた場合と10kgから11kgに増えた場合の結果変数への影響が異なるのであれば、何かしら「曲線的な関係性」が存在しているということである。
もちろんロジスティック回帰においても、交互作用を追加したり、曲線的な関係性を仮定したりといった分析もできるのだが、データマイニング屋からすれば「いちいち試行錯誤しないといけないなんてたいへんだね（笑）」といったところだろう。
一方、ニューラルネットワークやサポートベクターマシンという手法を用いれば、曲線的な関係性や交互作用も含め、最も識別力が高いと考えられる分類を行なうことができる。
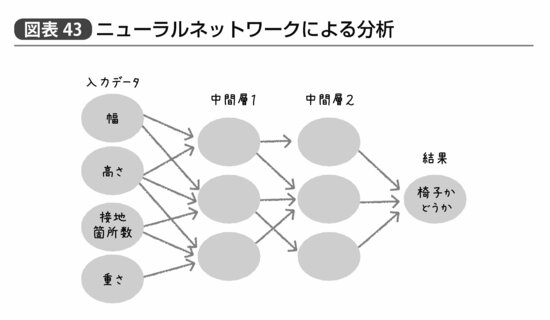
たとえばニューラルネットワークでは図表43のように入力データから「中間層」にあたる値を生み出す。中間層の数や中間層に含まれる変数の数はいくつに設定してもいいが、入力データからどの項目を用いて、それぞれどのような重みで中間層が算出されるか、というのは自動的に計算される。この楕円と矢印が神経細胞であるニューロンとその間の繋がりを模しているというのである。
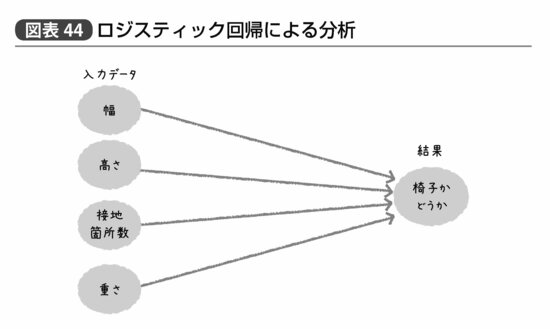
一方、（交互作用を使わない）ロジスティック回帰では単純に入力データから直接結果を予測する（図表44）。だからデータマイニングの専門家は回帰分析のことを「古臭い」とか「原始的」と思うのだ。
さらにサポートベクターマシンを用いれば、曲線的な方法で分類が可能になる。
図表45は仮に「高さ」と「重さ」というデータだけで椅子とテーブルを区別しようとした例だが、椅子は背もたれのあるなしによって「高さ」が2つに分かれる。そのため、テーブルは背もたれがない椅子よりは高く、背もたれがある椅子よりは低い。
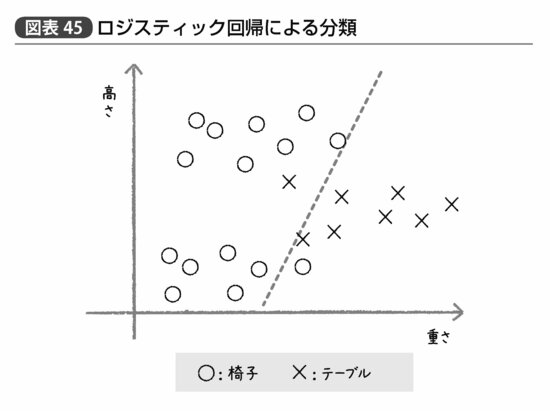
こうした状況でロジスティック回帰による分類を行なえば、点線で示すような直線のどちら側か、という判定を行なうことになり、一例ずつ椅子とテーブルを間違えて分類してしまうことになる。これがサポートベクターマシンを使って図表46のような曲線的分類を行なえばより正確ではないか、というのだ。
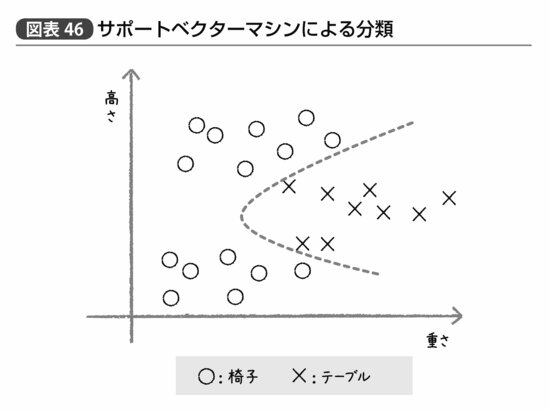
ニューラルネットワークにせよサポートベクターマシンにせよ、確かに曲線的あるいは複数の変数が絡む複雑な関連性がデータ間に存在しているのであれば回帰モデルよりも性能が高い。
「予測」に役立つデータマイニング
ただし、そのメリットを享受できるのはあくまで分類や予測だけが目的である場合、である。
単純なロジスティック回帰ではもとの説明変数と結果変数の関連性を簡単に把握することができる。図表44にロジスティック回帰によって求められたオッズ比を示せば、たとえば図表47のようになるだろう。
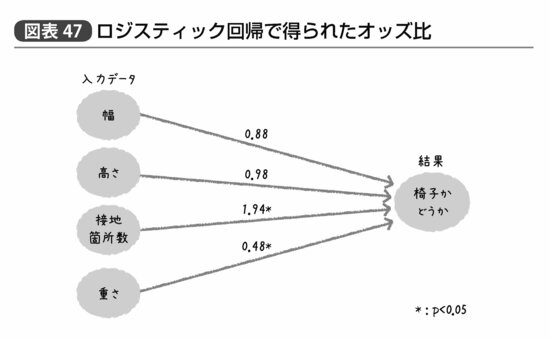
ある家具が椅子である確率は幅や高さによってはあまり変わらないが、接地箇所数が1つ増えるごとに約2倍、重さが1kg増えるごとに約半分になる、ということがわかれば、要するに「軽くて接地箇所数が多い家具」を選べば椅子である確率が高いことは誰でもわかるだろう。また一方で、幅や高さがあまり参考にならないのは、幅が広いベンチ的な椅子の存在や背もたれの有無のせいなのかもしれない。
これに対して、ニューラルネットワークの複雑な矢印がそれぞれどの程度の関連性を示しているか、あるいはサポートベクターマシンの曲線がどのような式で表されるか、といった結果は人間の目でわかりやすいものにはなっていない。そうすると、いくら予測の精度が高くても、「では実際にどうすればいいのか」というアクションが見えてこないということになる。
たとえばマーケティングであれば「来店頻度が高くてブランドに対してよいイメージを持っている顧客ほど購買金額が高かった」という結果が示されれば、頻繁に来店したくなるようなキャンペーンや、ブランドイメージを向上させる広告に投資してみようという次の施策が示唆されるだろう。だが「途中の計算はよくわかりませんが顧客の購買金額を予測できるプログラムが書けました」というのではどうしようもないのである。
もちろん顧客が購入するだろうという商品を予測するとか、退会しそうな顧客を事前に察知するとかいう、予測それ自体がゴールなのであればデータマイニングは有効である。こうした手法とロジスティック回帰の予測の精度を比較したところ、ほんの数パーセントも変わらなかった、ということもしばしばだが、その数パーセントが大きな利益に繋がるのであれば、データマイニングを選択すべきだろう。
しかしながら予測自体ではなく、予測モデルから今後何をすべきかを議論したいのであれば、回帰モデルのほうが役に立つ。こうした違いを理解したうえで適切な手法を選び分けることが、21世紀の統計家には求められるのである。
▶『マンガ 統計学が最強の学問である』の刊行に寄せて
『マンガ統計学が最強の学問である』は、言語化・定型化された仕事がAIに奪われていくなかで、「新たに何をするか考えて決める」スキルを日本に最大限広げるために制作されました。
実は初代『統計学が最強の学問である』はほとんど数式を使わず、統計学がどう生まれてどう役に立てられるのかにフォーカスした、統計学の本としては少し変わった本でした。しかし、40万部以上売れただけあって、あの本を読んで統計学を面白いと感じ、本格的に勉強しようとしたり、実務に活かすようになった、という方と私は日々の仕事の場で頻繁にお会いします。統計手法の数理面を細かく説明したり、統計解析をおこなうためのプログラミングに関する本は多数ありますが、それはちょうどAIのサポートが手厚くなっている部分です。今の時代はそれよりも、「統計学を活用したい」というモチベーション、「どのような課題に対して統計学を活用するか」という課題設定のコツ、そして分析結果の読み解き方と、結果を踏まえて何をやるべきかを考える枠組みといったスキルのほうが相対的に重要になってきているのではないでしょうか。
本書が目指すのは、まさにそうした今こそ必要な「統計学の活かし方」を、物語を通して皆さんにお伝えすることです。たとえば『SLAM DUNK』というマンガを読むことでバスケットボールをプレイするモチベーションが喚起されたり、バスケットボールの観方がわかるようになったりといった方がたくさんいるように、すばらしいマンガは多くの人の人生を変える力を持っています。ありがたいことに私にとっても大好きな漫画家であるうめさん（小沢高広さんと妹尾朝子さん）に漫画制作を依頼できたことで、ストーリー面でも作画面でもすばらしいものになりました。私自身のデータ活用に関わる経験を凝縮した物語を、うまく追体験していただければ幸いです。
また各話の最後には、それまでに出てきた統計手法について、できる限りわかりやすく、かつ簡潔に説明した解説を加えました。ストーリー内ではあまり説明臭くならないよう、しかし気になるであろう知識面はその後の解説で補足できるよう個人的にバランスをとったつもりです。
本書をきっかけに、さらに多くの人が統計学を学び、「新たに何をするか考えて決める仕事」をする力を手にしていただければ幸いです。
