データ分析で「1％の精度」に数千万円をかけるべきか？

統計学の解説書ながら42万部超えの異例のロングセラーとなっている『統計学が最強の学問である』。そのメッセージと知見の重要性は、統計学に支えられるAIが広く使われるようになった今、さらに増しています。そしてこのたび、ついに同書をベースにした『マンガ 統計学が最強の学問である』が発売されました。
第7回では、「正確なことを知るためには全数調査をしなければいけないのでは？」というサンプリング調査への「よくある反論」について考えます。（本記事は2013年に発行された『統計学が最強の学問である』を一部改変し公開しています。）

サンプリング調査への「よくある反論」

　正確なことを知るためには全数調査をしなければいけない、という素朴な感覚は多くの人間に備わっている。前節の失業率調査の話で言えば、たとえば仮にランダムに選ばれた全人口の0.5％を調査してその100％が失業者だったとしても、残りの99.5％全員が失業していなければ全体の失業率はわずか0.5％にしかならないのに、なぜ全人口の100％が失業者だなんていうことが言えるんだ、といった反論がサンプリング調査に対する「よくある反論」だ。

　この「よくある反論」で挙げられるような状況があり得るのかどうか、と言われると、厳密には「あり得なくはない」。ただし統計家は、ただ「あり得なくはない」と答えるだけではなく、「それがどの程度あり得るのか」についても必ず答えるだろう。

　真の失業率が0.5％で、全人口1億2000万人の0.5％である60万人を調査した結果、その全員がたまたま失業者である確率はもちろん0ではない。なぜなら1という数を64兆という数で10万回以上割った数のことを、数学では厳密には0と呼ばないからだ。

　もしこの確率をここで正確な小数にして表そうとすれば、少なくとも100万字以上、0という数字が並んだページをひたすらめくり続けることになるだろう。

　なぜこんな数字が出てくるのか意味がわからない人もいるかもしれないが、こう考えてみるといいかもしれない。わずか0.5％の確率、つまり200回に1回しか当たりの出ないくじを引いて、60万回一度も外れずに全部の当たりを引き続ける確率はどれほどだろう？

　当たりくじを引くたびに抽選箱に戻す、というやり方（統計学の専門用語では復元抽出と呼ばれる）は、戻さないやり方（こっちは非復元抽出）と比べてまだ確率が高いが、それでも「200分の1の60万乗」という奇跡が必要になる。これが先ほどの64兆の10万乗分の1という話である。

　ちなみに復元抽出では60万回のチャレンジの間ずっと「200分の1」という一定の当たり確率が維持されるが、実際の失業率調査は非復元抽出であり、最後60万回目のチャレンジにおける当たり確率は残り約1億1940万人中1人と、それだけで奇跡とも言える数字になる。実際にはこの64兆の10万乗分の1という天文学的な値ですら生ぬるいのである。

　こう考えたうえで、本気でこの奇跡の心配をして「よくある反論」をする人はよっぽど悲観的な人か、あるいは平然とイカサマをやってのける詐欺師と言えるだろう。「巨大隕石が今この瞬間にここに落ちてくるリスク」が心配されることはないのに、なぜ極端にサンプリングが偏って「調査が当てにならないものである確率」が心配されるのだろうか。

　さすがに0.5％の当たりを引き続けることは非現実的だと思うかもしれないが、仮にこの当たりの確率が99％だったとしても60万回当て続けるのは生やさしいものではない。600回当て続ける確率ですら0.24％ほどの確率しかなく、60万回というとそのさらに1000乗という奇跡的な確率になるのである。

　計算過程を簡単にするために「調査した対象全員が当たりになる確率」という事例を例として見せたが、仮にそうでなかったとしても10万人も調査すれば真の値と調査結果から示された値の間にほんの1％の乖離が生じる確率すら奇跡的なものになる。

誤差を計算する方法

　なお実際の誤差の計算は、こうした直接的な確率の計算ではなく図表7の式で表される。

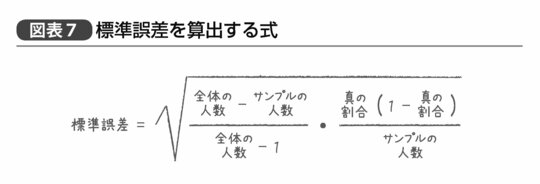
　たとえば先ほどの例で言えば、全体の人数とは国民の全人口である1億2000万人という数が入り、真の割合には「真の失業率」の値が入る。もちろんこの値は実際にはわからないが、サンプル調査から得られた失業率の値を入れてもほぼ間違いではない。

　もし心配であれば、「標準誤差」は真の割合が50％のときに最大化するので、試しにその値を入れてみて「考えられる最大の標準誤差」を考えておくという慎重なやり方もある。

　ちなみになぜ割合が50％のときに標準誤差が最大となるかというと、0.5 ×（1 － 0.5）が、0.6 ×（1 － 0.6）だが、だとか、0.3 ×（1 － 0.3）より大きい、という計算からなんとなくはわかってもらえると思う。

　この標準誤差というのがどういったものかというと、サンプルから得られた割合（たとえば失業率）に対して標準誤差の2倍を引いた値から標準誤差の2倍を足した値までの範囲に真の値が含まれている信頼性が約95％、という値である。

　たとえばサンプリング失業率が25％という調査結果が得られ、その標準誤差が0.5％だったとすれば、全数調査をした結果得られるであろう真の失業率も24％～26％の間にあると考えてほぼ間違いない、ということを統計学者たちは80年以上前に証明しているのだ。

サンプルを1万増やしても標準誤差は0.1％しか変わらない

　なお、数式なんて見たくもない、という人向けに実際どの程度標準誤差が変わるのか、という結果もお見せしておきたい。たとえば10万人の顧客のデータからその男女別割合を調べた結果、顧客に占める女性の割合が70％だったと仮定しよう。その標準誤差は、何人をサンプリングすればどの程度になるのか、を調べた結果を示すと図表8のグラフのようになる。

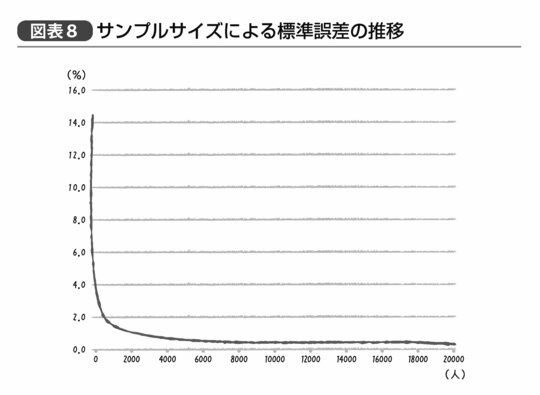
　サンプルサイズすなわち、調べるデータの件数が10万人のうち100名分しかなければその標準誤差は4.6％にもなり、得られた「顧客に占める女性の割合が70％」という結果が実際には「女性の割合が61％～79％と考えてほぼ間違いない」という解釈になってしまう。しかし、1000名いれば標準誤差は1.4％となり「女性の割合が67％～73％と考えてほぼ間違いない」、8000名を超えて標準誤差が0.5％となると「女性の割合が69％～71％と考えてほぼ間違いない」ということになる。

　そして逆に、このあたりから先は、「サンプルサイズを倍に増やしてもあまり誤差が小さくならない」ということになっている（なお、1万名分使っても標準誤差は0.4％で、2万名分でも0.3％にしかならない）。

　この結果と、高価なデータ処理サーバに投資して得られる「女性の割合がちょうど70％です」という結果を比べたときに、果たしてとるべき判断はどれほど異なってくるだろう。

　8000名分の顧客データをランダムに抽出してアウトプットするだけならデータベースを管理する技術者がちょっと調べればすぐに実現できるし、8000名分のデータの集計表をエクセルで書くぐらい、アルバイトの学生にだってものの数分でできることだ。技術者の残業代と学生のアルバイト代を合わせてもほんの数万円で済んでしまうかもしれない。そこからほんの1％やそこらの精度を改善することは、果たして数千万円も投資する価値のあるクリティカルな影響を持つのだろうか？

　もしその答えが「Yes」なら、その会社は間違いなくビッグデータ技術に投資を惜しむべきではない。だが、もし「No」と答える会社なら、数千万円分の投資のうちいくらか、あるいはそのすべてについて、お金をドブに捨てるようなものと言えるのかもしれない。

まずは、正しい判断に必要な最小十分のデータを

　ビッグデータ時代と呼ばれる考え方に逆行するようだが、私は誰からデータ分析の相談を受けても「まず正しい判断に必要な最小十分のデータを扱うこと」を推奨している。もし1％の誤差が今後数年積み重なって何千万円分もの売上やコストに繋がるのであれば、ビッグデータ解析技術は役に立つだろう。だがその場合においても、必ずしも最初からすべての解析を全データで行なう必要はないのだ。

　データ分析という過程はしばしば探索的な作業を必要とする。元のデータが複雑であればあるほど、実際にやってみたら明らかに理屈と反する結果が出たから念のため違う解析手法を試してみる、とか、使用したデータ自体に何らかの問題があることがわかったためにその修正が必要になる、といったことは熟練した統計家であっても避けることができない。というか、むしろ熟練した統計家ほど誤りを犯さないためにこうした予備的解析の労を惜しまないと言っても過言ではない。

　結果を見ながらいろいろな手法やデータの切り口を試すという探索的解析においては、特にトライ＆エラーの回数が重要になる。そのため、特殊なツールを使ってトリッキーなプログラムを組まなければいけない事態も、解析のための操作からレスポンスまでに長時間待たされる事態も可能であれば避けたい。そうなると、たとえ最終的には全データを対象とした分析や検証が必要となるにしても、やはりまずは適切なサイズのサンプリングデータを使って、探索的解析で仮説の目星をつけたほうがいい。

　必要な仮説を見つけるための適切なサイズとサンプリング方法については、それなりに専門的な統計学の知識が必要になるが、とりあえずデータの概観を掴むだけならまず数千～1万件ほど抽出していじってみればいいし、それくらいならエクセルぐらいしか使えない人であっても十分にできる仕事である。

　もちろん莫大なデータから高速で一定条件のランダムサンプリングをするときにも、最終的な解析結果の妥当性を検証する際にも、ビッグデータ技術は活躍するだろう。だが果たしてその速度と精度にどの程度の価値があるのか？ と聞かれれば、それは解析結果からどれだけの価値を得られるのかによる、としか答えられない。

　解析はそれ自体価値があるものではなく、それを活かして何を行ない、どれだけの価値を得られそうなのかによって異なるのである。