今、世界最先端のIT産業を支えているのは、インド人エンジニアたちです。なぜインドが多くの優秀なエンジニアを輩出しているか、その秘密はインド独特の算数教育に隠されています。インドの小学校の算数の授業は、日本の九九(くく)のようにただ暗記させるだけでなく、なぜそうなるかを考えさせる学習法が基本になっています。どのように計算したらより効率良く正しい答えを導き出せるか、子どもたち自身が考えながら学んでいくことで算数が面白くなり、さらに自発的に勉強が進むようになるわけです。
この連載ではそのインド式計算法をわかりやすく学べる本『子供のインド式「かんたん」計算ドリル』の中から具体的な計算方法を紹介していきます。子どもたちの自宅学習用にピッタリのうえ、大人にとっても目からウロコの計算法です。ぜひ親子で楽しく学んでください。第2回は少し複雑な2けたのかけ算をあっという間に解く方法をご紹介します!(初出:2020年3月27日)
19×19までの計算が
5分で覚えられる!
日本の小学校の算数教育で最も重要なテーマは「九九(くく)」の習得でしょう。子どもたちは九九を覚えるのに四苦八苦です。しかしインドの小学生は、なんと1~19どうしのかけ算を瞬時に答えるというのです。九九の81通りに対して19までのかけ算は361通り。これをすべて暗記するのは小学生にとっては大変なことのはず。
ですが、これにはコツがあるのです。『子供のインド式「かんたん」計算ドリル』からご紹介するインド式計算法を用いれば、誰もが簡単に19×19までのかけ算を解くことができます。
では、まず一例として「13×12」を解いてみましょう。
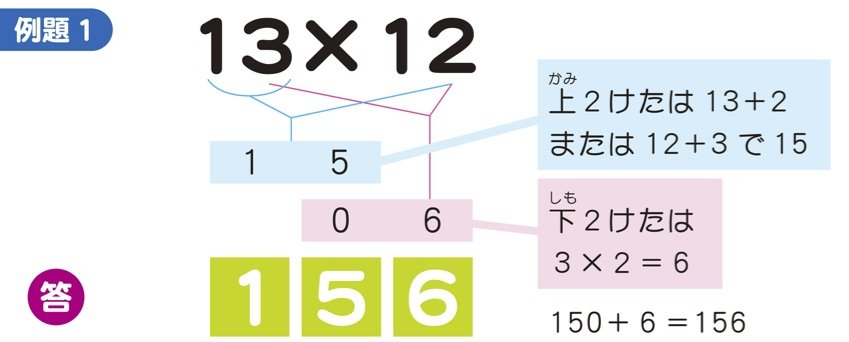
【例題1】の図のように、まずどちらかの2けたの数字と、もうひとつの数の1の位の数字をたしましょう。13+2(または12+3)で15になります。この数字が100の位と10の位の数になります。つまり150です。次に1の位の数字どうしをかけてください。3×2=6、これをさきほどの数にたして150+6=156が答えになります。
次は1の位をかけた数が2けたになる場合を考えてみましょう。
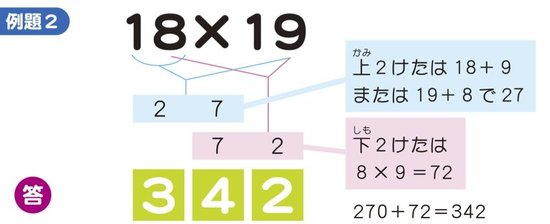
【例題2】を見てください。【例題1】と同じように、まずどちらかの2けたの数字と、もうひとつの数の1の位の数字をたしましょう。18+9(または19+8)=27 この数字が100の位と10の位の数になります。つまり270です。これに1の位の数字どうしをかけた8×9=72をたしてください。270+72=342が答えになります。
では【例題1】が、なぜ紹介したような計算方法で解けるのか、今回も四角形の面積として考えて説明してみましょう。
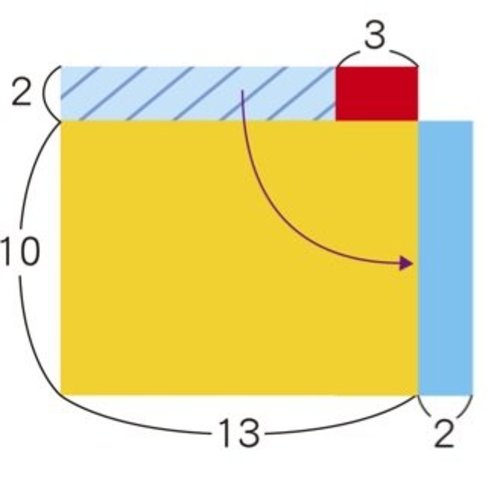
まず赤い部分が下2けたの面積です。3×2で6になります。
上2けたは黄の部分と青の部分をたした面積になります。青の部分を移動すると分かりやすくなります。(13+2)×10=150
赤、黄、青の3つの面積の合計は、6+150=156となります。
それでは、19×19までのかけ算を実際にやってみましょう。以下の問題をインド式計算法で解いてみてください。手順を覚えてもらいたいので、前回同様に薄い赤文字でヒントを入れておきます。
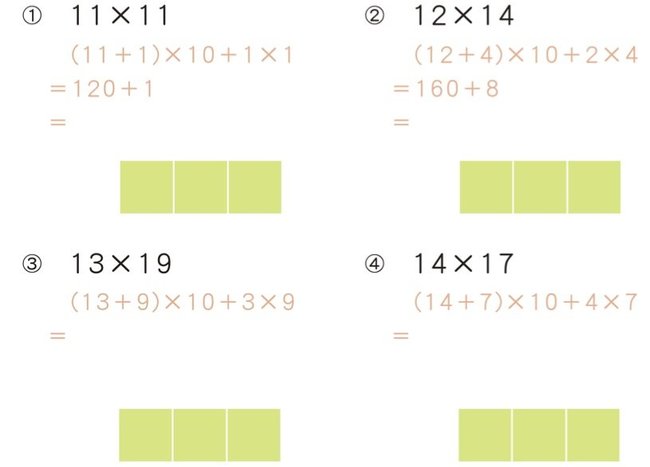
問題の答えは以下のようになります。
(1)121 (2)168 (3)247 (4)238
次はいまの形を応用して、11~19とそれ以上の数のかけ算の計算法をご紹介しましょう。例として「14×28」を考えてみます。
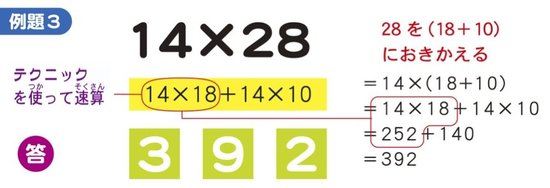
この【例題3】でも、11~19どうしのかけ算を計算するときのテクニックを使います。28を(18+10)と置きかえると、14×28=14×(18+10)=14×18+140=(14+8)×10+(4×8)+140=252+140となり、392が答えとわかります。
それでは、11~19とそれ以上の数のかけ算を実際にやってみましょう。こちらも薄い赤文字でヒントを入れておきます。
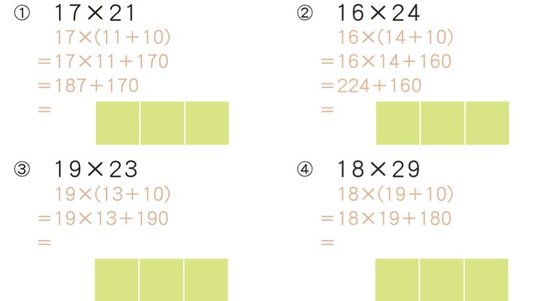
問題の答えは以下のようになります。
(1)357 (2)384 (3)437 (4)522
このように工夫することで、少し複雑な計算も暗算で解けるようになるわけです。では、次回も新しい計算テクニックをご紹介しますのでお楽しみに。
(続く)


