今、世界最先端のIT産業を支えているのは、インド人エンジニアたちです。なぜインドが多くの優秀なエンジニアを輩出しているか、その秘密はインド独特の算数教育に隠されています。インドの小学校の算数の授業は、日本の九九(くく)のようにただ暗記させるだけでなく、なぜそうなるかを考えさせる学習法が基本になっています。どのように計算したらより効率良く正しい答えを導き出せるか、子どもたち自身が考えながら学んでいくことで算数が面白くなり、さらに自発的に勉強が進むようになるわけです。
この連載ではそのインド式計算法をわかりやすく学べる本『子供のインド式「かんたん」計算ドリル』の中から具体的な計算方法を紹介していきます。子どもたちの自宅学習用にピッタリのうえ、大人にとっても目からウロコの計算法です。ぜひ親子で楽しく学んでください。第3回は、難しい2けたのかけ算も暗算で解ける秘密の方法を紹介します!(初出:2020年3月31日)
難しい2けたのかけ算も
暗算できる秘密のテクニック
前回は、少し複雑な2けたのかけ算をかんたんに解く方法をご紹介しました。実はこうした計算のテクニックは普段の勉強や受験にも役立つのです。算数の計算は工夫することでより早く答えが導き出せます。受験塾などでは、効率よく計算する様々なテクニックを伝授しています。
しかし本当に重要なのは単にテクニックを覚えることではありません。考えて計算方法を工夫することで、より算数が楽しくなるのです。
今回は、さらに難しい2けたのかけ算を暗算できる秘密の方法を伝授します。秘密のカギは2けたの数のどちらかの1の位を0にして考えることです。

かけ算をするとき、どちらかの数が10や20のようにきりのいい数字だと計算しやすくなりますね。これはそれを利用した計算法なのです。
【例題1】では、12を10+2と考えます。
17×12=17×(10+2)=170+34=204 と簡単に計算することができます。
次はひき算をうまく使った例題をあげてみます。
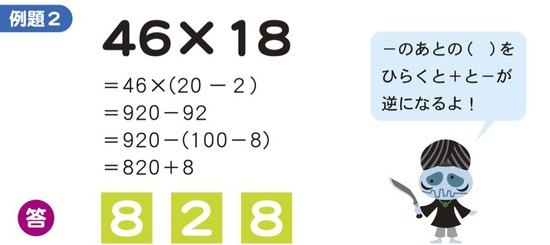
【例題2】の場合は、18を20ー2と考えます。
46×18=46×(20ー2)ですから、46×20=920、ここから46×2=92を引いて、920ー92
ここでさらにテクニックを使ってみましょう。
92を(100ー8)と置きかえると、さらに簡単に計算できるのです。920から100を引いて820、これに8をたして828が答えになります。
では今回も【例題1】で、なぜこのような計算方法になるのか、四角形の面積で考えてみましょう。
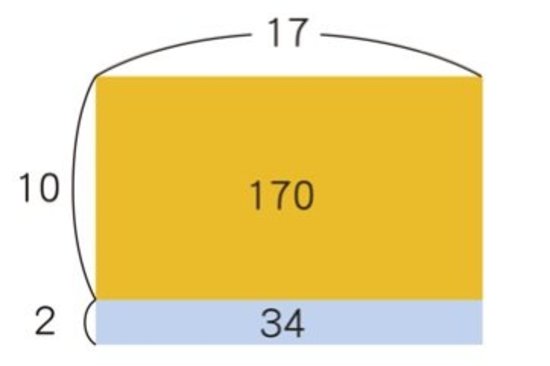
12を10(黄の部分)と2(青の部分)に分けて考えます。
黄の部分の面積は17×10=170 青の部分の面積は17×2=34 全体の面積は、170+34=204 となるわけです。
それでは、2けたの数の1の位を0にする方法で実際に問題を解いてみましょう。今回も手順を覚えていただきたいので、薄い赤文字でヒントを入れておきます。
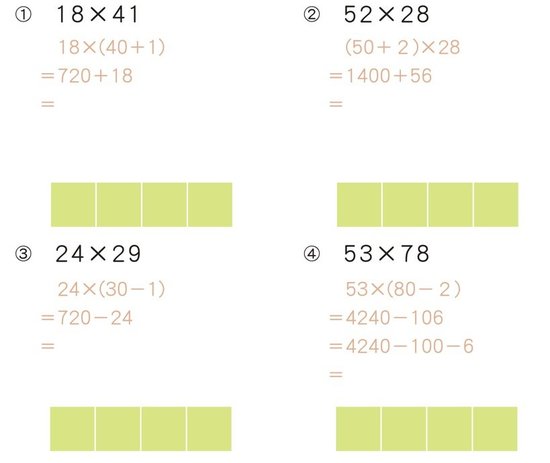
問題の答えは以下のようになります。
(1)738 (2)1456 (3)696 (4)4134
では、これまで『子供のインド式「かんたん」計算ドリル』から学んだ計算方法を使って、以下の練習問題を解いてみてください。
(1)12×13=
(2)15×19=
(3)11×19=
(4)16×17=
(5)15×15=
(6)11×16=
(7)17×17=
(8)13×21=
(9)17×23=
(10)19×26=
(11)23×21=
(12)61×14=
(13)52×12=
(14)39×49=
(15)18×19=
(16)25×58=
(17)55×19=
(18)27×92=
(19)18×62=
(20)87×98=
問題の答えは以下のようになります。
(1)156 (2)285 (3)209 (4)272 (5)225 (6)176 (7)289 (8)273 (9)391 (10)494 (11)483 (12)854 (13)624 (14)1911 (15)342 (16)1450 (17)1045 (18)2484 (19)1116 (20)8526
いかがですか。慣れないうちは時間がかかると思います。けれど、何度も繰り返し練習するうちにテクニックが身につき、より早く計算ができるようになるはずです。頑張ってください!



