今、世界最先端のIT産業を支えているのは、インド人エンジニアたちです。なぜインドが多くの優秀なエンジニアを輩出しているか、その秘密はインド独特の算数教育に隠されています。インドの小学校の算数の授業は、日本の九九(くく)のようにただ暗記させるだけでなく、なぜそうなるかを考えさせる学習法が基本になっています。どのように計算したらより効率良く正しい答えを導き出せるか、子どもたち自身が考えながら学んでいくことで算数が面白くなり、さらに自発的に勉強が進むようになるわけです。
この連載ではそのインド式計算法をわかりやすく学べる本『子供のインド式「かんたん」計算ドリル』の中から具体的な計算方法を紹介していきます。子どもたちの自宅学習用にピッタリのうえ、大人にとっても目からウロコの計算法です。ぜひ親子で楽しんでみてください。
かけ算は四角形の面積だと考えよう
一見むずかしそうな計算も少し工夫することで、驚くほど簡単に解けてしまいます。そのためには「公式がなぜそうなるのか」をきちんと理解しておくことが大切です。
かけ算とは四角形の面積を求めることと同じです。2つの数はタテとヨコの2辺で、その辺で作られる四角形のなかにある小さな正方形の数が面積になると考えればよいでしょう。下の図のように3×6であれば、18個の小さな正方形の集まりということができます。
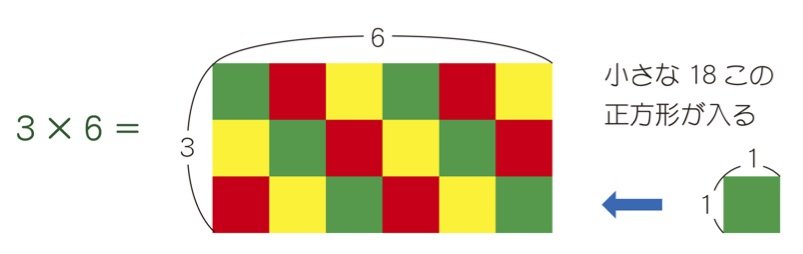
九九(くく)では、3×6=18は「さぶろくじゅうはち」と覚えますが、もし九九を忘れても3×6とは、タテ3、ヨコ6の四角形の面積であることを理解しておけば、困ることはないのです。
あるいはかけ算をたし算におきかえることもできます。つまり3×6は3を6回、あるいは6を3回たせばいいのです。
3×6
=3+3+3+3+3+3
=6+6+6
もちろん、2けたどうしのかけ算でもこの法則が使えます。
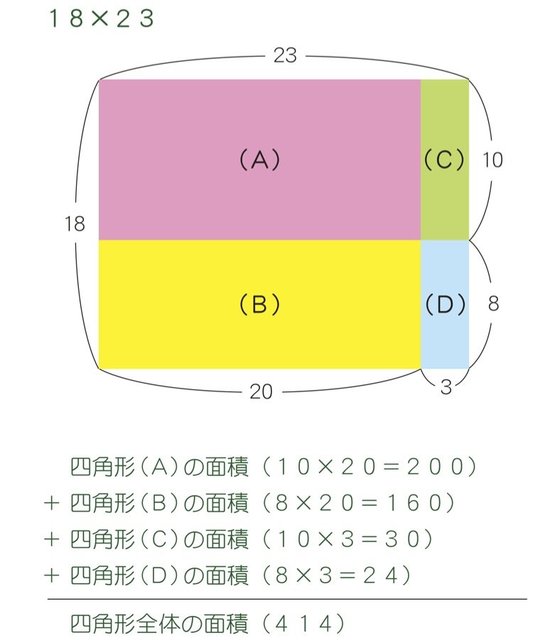
たとえば18×23を求めるとき、下の図のような1辺が18と23の長方形の面積を考えてみましょう。そしてきりのいい10と20のところで直線をひいて4つの四角形にわけます。それぞれの面積の合計が、全体の面積になるのです。この考えが『子供のインド式「かんたん」計算ドリル』で紹介するインド式計算法の基本になります。
それでは実際にインド式の計算方法を紹介していきましょう。まず、もっともわかりやすい「2けたの数字×11」のかけ算のやり方をみていきましょう。
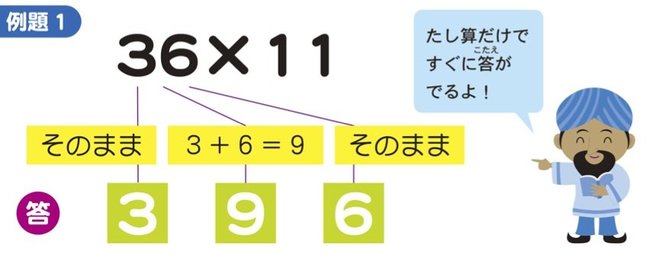
【例題1】のように36×11なら、「11」でないほうの数「36」に注目してください。まず、1の位はそのまま1の位の数字を書きます。10の位は2けたの2つの数をたした数字(この場合は3+6=9)、そして36の10の位の3が100の位になるのです。これで答えは「396」になります。
ではもう1問、例題をあげてみましょう。
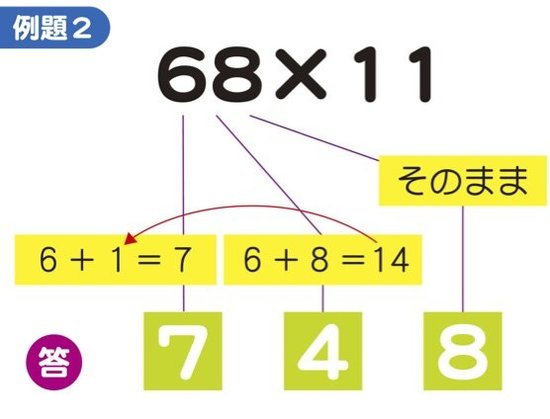
【例題2】を見てみましょう。1の位は68の8がそのまま入ります。10の位は6+8で14の4が入り、100の位に1くりあがって6+1=7。答えは「748」となるわけです。
では、なぜこのような計算方法になるのか、【例題1】の36×11を四角形の面積として考えて説明します。

上の図の赤い部分は1の位の面積です。6×1で6になります。
黄色の部分は10の位の面積です。6×10+30×1=(6+3)×10=90 つまり10の位は6+3になるわけです。
水色の部分は100の位の面積です。30×10=300 100の位は3となります。
この3つの面積をたすと、6+90+300=396となります。
では、「2けたの数字×11」のかけ算を実際にやってみましょう。以下の問題をインド式計算法で解いてみてください。まずは手順を覚えてもらいたいので、薄い赤文字でヒントを入れておきます。
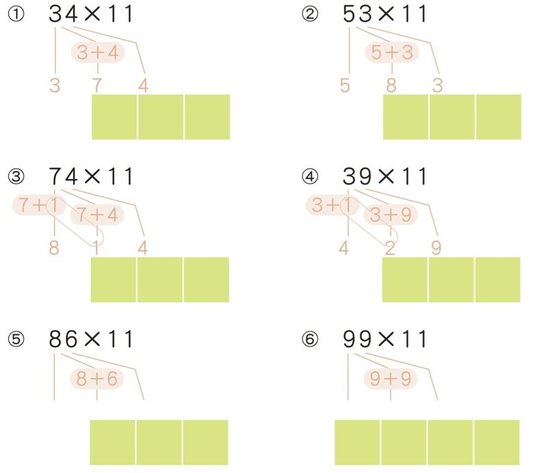
問題の答えは以下のようになります。
(1)374 (2)583 (3)814 (4)429 (5)946 (6)1089
どうでしたか。慣れてくると「2けたの数字×11」のかけ算はすぐに暗算でできるようになるはずです。それでは次回は、「19×19までの暗算が5分で覚えられる」方法を紹介します。
(続く)



