即答できますか？「あなたの髪の毛」はざっくり何本？

「フェルミ推定」は、調べても正確な答えがわからないような一見難解な問題だ。
でも、地頭のいい人はわずかな手がかりだけでパッと概算することができる！
本連載では、ビジネスでも日常のひとコマでも使える超・高速計算テクニックと、どんな難問でも自分なりの答えを導くコツを紹介したイギリスで話題の1冊、『世界の猫はざっくり何匹？　頭のいい計算力が身につく「フェルミ推定」超入門』より一部を特別に公開する。

大人の髪の毛の本数は？

　髪の毛の本数は、もちろん人によってかなり違う。そこで、たとえばふさふさな人の本数をはじき出してみよう。しかも、頭皮を調べずに想像力だけでだ。

　人間の頭皮1平方センチメートルをイメージしてみてほしい（できるだろうか？）。

　毛穴と毛穴はどのくらい離れているだろうか？ まずは上限と下限を考えてみよう。2ミリメートルも離れていたら髪の毛はまばらで、頭皮が透けて見えてしまうだろう。でも0.5ミリメートルしか離れていなかったら、頭皮はびっしりと覆われて、まるで毛皮のようになってしまうだろう。そこで、理にかなった妥協点として1ミリメートルとしてみよう。

　すると、頭皮1平方センチメートルの中に10×10＝100個の毛穴があることになる。

　では頭皮の面積は？ 自分の頭のまわりに両手を回して、人差し指をおでこのてっぺんに合わせ、親指を首と頭のつなぎ目に合わせてみよう。そうしてできた円の直径は25センチメートルくらいだろうか。

　直径25センチメートルの円の面積はπ×半径の2乗で、半径は12.5センチメートル。でもすべておおざっぱなので、ジコールの出番だ。（ジコールについては本連載の第3回『イギリスで話題の数学者が伝授！誰でも超高速で計算できるワザとは？』をご覧ください）

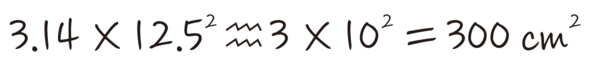
　頭皮は円ではなくて、どちらかというと半球に近い。半径が同じであれば円よりも半球のほうが面積が広いので、2倍して600平方センチメートルとしよう。

　したがってこの概算によれば、典型的な人の頭部に生えている髪の毛の本数は600×100＝60000本となる。

　この値にはかなりのばらつきがあるだろう。最大で100000本、最小で30000本かもしれない（おでこの生え際が後退していて髪も薄くなりはじめている人は除く）。

　1人の人が最大でも100000本しか髪の毛を生やしていないという情報に基づけば、たとえばイングランド北部の街ハッダースフィールドにはまったく同じ本数の髪の毛を生やしている人が2人以上いると、絶対的に確信を持って言うことができる。

　それを証明するには、まずハッダースフィールドの住民全員が髪の毛の本数が違うと仮定する。髪の毛が一番多い人の本数は約100000本だと分かっている。そこで、それ以外のすべての人はもっと本数が少ないと仮定しよう。また、全員の本数が違うと仮定した。そこで、髪の毛が1本もない人を先頭に立たせて、次に1本の人、2本の人という具合に、全員を1列に並べたとイメージする。

　髪の毛の本数がそれぞれ違う100000人の人が並んでいる。では100001人目の人はどうすればいいのか？ あるいはハッダースフィールドの場合、残り50000人以上の住民は？

　誰かと本数が一致してしまうのは、避けようがない。だから、ハッダースフィールドでは少なくとも2人の人が同じ本数の髪の毛を生やしているはずで、それどころか、誰かと本数が一致する人が何万人もいることが証明された。

　このようなタイプの証明を「鳩の巣原理」といって、髪の毛を数えるのよりもかなり抽象的な問題に答えるのに数学者がよく使っている。

（本原稿は『世界の猫はざっくり何匹？　頭のいい計算力が身につく「フェルミ推定」超入門』ロブ・イースタウェイ著、水谷淳訳の抜粋です）