回帰分析を超本質的に解説する

統計学の解説書ながら42万部超えの異例のロングセラーとなっている『統計学が最強の学問である』。そのメッセージと知見の重要性は、統計学に支えられるAIが広く使われるようになった今、さらに増しています。そしてこのたび、ついに同書をベースにした『マンガ 統計学が最強の学問である』が発売されました。第19回では、統計学の最も重要な手法の1つである回帰分析について解説します。（本記事は2013年に発行された『統計学が最強の学問である』を一部改変し公開しています。）

回帰分析とは何か

　ケースコントロール研究のようにわざわざデータの取り方を工夫しなくても、より高度な手法を用いれば可能な限り条件を揃えた「フェアな比較」が可能になる。そのための最も重要な枠組みの1つが回帰分析だ。

　大学の統計学の教科書を読めば、t検定だとかカイ二乗検定だとか、分散分析だとか回帰分析だとかいう手法が必ず登場する。しかしながらこれらの統計手法はすべて、大きく言えば「一般化線形モデル」という広義の回帰分析の考え方で統一的に理解できることが、1972年にネルダーとウェダーバーンという2人の統計学者によって示されている。データ間の関連性を示し、それが誤差と呼べる範囲なのかどうかを検定する手法はすべて、大きな枠組で言えば回帰分析の一種であると考えられるのだ。

　だが、こうした回帰分析というものはなぜ必要なのだろうか。データを用いなくても我々は経験から傾向性や法則性を学びとることができる。それを「ジンクス」や「理論」や「成功の方程式」などと呼んでいる人もいるだろう。

　じつは回帰分析がなぜ必要か、という質問に対する答えは、そもそもこの手法につけられた「回帰」とはどういう意味かということが関わってくる。そこで本節はこの「回帰」という現象が発見された歴史について説明しよう。

背の低い野村くんの恋愛

　私が世界で最初の回帰分析の話を聞いたときに思い出したのは、中高時代の友人である野村くんのことだった。

　彼は当時、自分より背の低い女子としか付き合おうとしなかった。彼自身かなり小柄なので、相手の女子も必然的に限られてくる。当時一緒に遊んでいた友達の中には小林さんという170cm近い身長の女子もいたが、彼女のような女性は完璧に恋愛対象外である。

　私は当時学校でチャールズ・ダーウィンの進化論を教わったこともあって、野村くんのような男のせいで人類は2種類に別れてしまうのではないかと危惧した。

　念のためダーウィンの進化論について確認しておくと、おおよそ以下のようなものである。

・生物の個体は同じ種でも微妙に違う
・個体の特徴は親から子どもに遺伝する
・特徴の中には生存や繁殖に有利なものもある
・生存や繁殖に有利な特徴を持った個体は世代を経るごとに増加する（逆に不利なものは淘汰される）
・ただしどのような特徴が繁殖や生存に有利なのかは環境によって異なる

　かくして生物は世代を経るごとに環境に適した特徴を持つに至るのである。ダーウィンは帆船で世界を一周するなかで、たとえば同じ種の小鳥でも微妙にくちばしの形が異なることを発見し、その答えとして進化論というアイディアを著書である『種の起源』に示した。

　もし野村くんのような考え方のせいで、身長が高い女性は自分より身長の高い男性としか結婚せず、身長が低い男性は自分より低い身長の女性としか結婚しないとする。当然、身長の高い両親の子どもはより高身長になるだろうし、身長の低い両親の子どもはより低い身長となるだろう。

　こうした遺伝が繰り返されるとすれば、いずれ人類の身長は二極化していくのではないだろうか？ きっと馬とロバが近縁種でありながら大小の違う生物に別れてしまった背後にも、こうした理屈があるのではないだろうか？

　別にこれは頭のおかしな高校生の妄想などではなく、フィッシャーを含めて、彼の時代の統計学者の多くはこの仮説に本気で取り組んでいた。というか、当時生まれた統計学的手法の多くが、こうした進化論的な考え方の検証のために生みだされていたと言っていい。フィッシャーがメンデルの研究にイチャモンをつけたのも、彼自身が統計学者であると同時に遺伝学や生物学の研究にも関心を寄せていたためである。

ダーウィンの従兄弟と優生学

　こうした生物を分析するための統計学、という流れを作ったのはダーウィンの従兄弟であるフランシス・ゴルトンである。彼は高校生の頃の私と同様、と言ってはずいぶん語弊があるかもしれないが、ダーウィンの進化論というアイディアに触発された。

　ゴルトンが思いついたのは、この進化論の人間への応用である。彼は1883年に著した『人間の知性とその発達』において、「より環境に適した人種や血統を優先して、より多くの機会を与える」という、優生学の考え方を提示した。

　優生学とはすなわち、人間の知性は遺伝によって決定されるのだから、積極的に知性の低い人間は淘汰し、知性の高い人間ができるだけ多くの子孫を残すようにすれば人類の知性はどんどん向上していくから、これが人類の目指すべき正義ではないかというのだ。

　こうした彼の思想はその後しばらく欧米で大流行することになる。たとえば19世紀後半から20世紀にかけてのイギリスでは、中流階級以上の裕福な人々を中心に、「政府による不適切な援助や慈善事業によって無能な人々が増えてしまう」という事態を非効率だとして問題視する考え方が存在していた。

　優生学の考え方が現在タブーとされているのはナチスが本気でこの思想を信じ、あるいは利用し、「劣等人種」の虐殺に繋がったからだと言われている。ただし、日本においても遺伝的な障害のある者に対して生殖を不能にすることを認めた優生保護法が廃止されたのは比較的最近、1996年のことである。ナチスだけを悪者にはできない。このような法律はかつて世界中に存在しており、その背後には多かれ少なかれ優生学の考え方があった。

「平凡への回帰」の発見

　しかしながら、倫理的な議論以前に「そううまくいくわけではない」ということは、ゴルトン自身やゴルトンの弟子たちが自らの研究で実証していたのである。

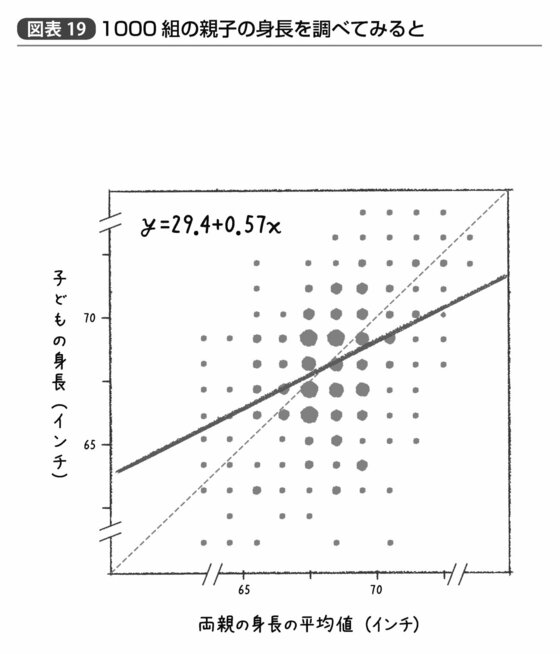
　その結果を示すのが図表19だ。

　ゴルトンの興味は人間の知性に関する遺伝の法則にあったが、フランスの心理学者ビネーが、いわゆるIQの元となった知能検査を発明するのはもう少し後の時代の話である。

　IQという言葉は現在当たり前のように使われるが、知性という見も触れもしない抽象的な概念の測定は、近代以降の心理学や統計学の進歩によってはじめて可能になったことである。ゴルトンが知性を統計解析しようにも、そのデータ自体が当時は得られない。だから、代わりにゴルトンは、約1000組の親子の身長を測定し「優秀な親から優秀な子どもが生まれる」という現象を実証しようと試みた。その結果が図表19に示されている通りだ。

　横軸に両親の身長の平均値、縦軸にその子どもの身長がそれぞれインチ単位でとられ、丸の大きさは該当する人数の多さを示している。

　そして左下から右上に向かう点線が、「両親の身長の平均値＝子どもの身長」となるのではないかと仮定した理論上の関係性を示す線である。一方それより角度の緩やかな実線で示す直線が、実際のデータの中心を通る、すなわち「両親の身長から子どもの身長を最も小さな誤差で予測する」直線である。この直線は左上に表記されたという数式で表される。イギリスにおける1インチは2.54cmであるので、これを現代風にセンチメートル単位で表記すれば29.4×2.54＝74.7という計算から次のようになるだろう。

子どもの身長（cm）＝74.7（cm）＋0.57×両親の身長の平均値（cm）

　このようにデータ間の関係性を記述する、あるいは一方のデータから他方のデータを予測する数式を推定するのが回帰分析という考え方であり、こうした数式で記述される直線のことは回帰直線と呼ぶ。重要なのはこの実線で示された実際の関係性と、点線で示された理論上の関係性の違いだ。

　グラフの左側、つまり両親の身長が平均より低いグループにおいては、理論上の関係性を示す点線よりも実際の関係性を示す実線のほうが高い。一方でグラフの右側、つまり両親の身長が平均より高いグループにおいては、実際の関係性を示す実線のほうが低い。

　これはどういうことだろうか。親と子どもの身長が似ることは古代から誰でも経験的に知っていただろうが、身長が高い親の子どもほど実際にはそれほど高くない、とか、身長が低い親の子どもだって実際にはそれほど低くない、なんていう結果はゴルトンがデータを分析してみせるまでほとんど考えられたことがなかった。

　こうした現象のことをゴルトンは「平凡への回帰」と呼び、後に彼の弟子や影響を受けた統計学者たちによって「平均値への回帰」と呼ばれるようになった。実際のデータは、理論上の推測よりも「平均値に近づく」という意味である。

　これを先ほどの自分の同級生のたとえで言うならば、「小柄な野村くんの息子は野村くんよりも背が高い」、一方で「高身長な小林さんの娘は小林さんよりも背が低い」という可能性が高いということである。

　身長という測定誤差が小さく遺伝的要素が強いものでさえそうなのだから、知能についてはなおさらなのだろう。知能の高い両親から生まれた子どものほうが平均的には知能も高いのかもしれないが、それだけで十分予測ができるかというとそれほどでもない。だから人類は二極化するような進化をすることもないし、遺伝や人種に基づいて人間を差別するメリットもないのである。

「オリンピックの魔物」の正体

　なぜこうした「平均値への回帰」という現象が起こるかと言えば、それは身長だろうが知能だろうが、あるいは生物の特徴だけに限らず、この世のすべての現象がさまざまな「バラつき」を持っているからだ。

　少し具体的な事例としてオリンピックの代表選びを考えよう。

　直前の予選大会で素晴らしい記録を叩き出すことができた選手を国の代表として送り出すものの、実際には思ったほど記録が伸びず残念な結果に終わる、という状況を我々は毎大会のように目にすることができる。これも平均値への回帰の一例であり、スポーツの結果がバラつきを持っているために生じる現象である。

　スポーツの結果は実力だけで決まるわけではない。100メートル走のように単純な競技でさえ、大会ごとに記録は異なる。仮にそのバラつきを左右するものをコンディションと呼ぶとすると、直前の大会だけでたまたまよい記録を出せた人の多くは、本人史上まれに見るレベルの好コンディションであった可能性が高い。

　だが、そうした好コンディション込みの記録をもとに本番の結果を予測する、というのは「奇跡がたまたま2回起きる」というような虫のよすぎる結果を期待しているに等しい。こうした選手たちが本番において平凡なコンディションとなるか、あるいは絶不調になるかまではわからないが、少なくとも奇跡的な好記録よりは「平均値へ回帰」する結果となるはずなのだ。もちろん逆に、本大会直前に絶不調だった選手にしても、「それよりはマシである可能性が高い」という逆向きの平均値への回帰が考えられる。

　オリンピックの魔物と呼ばれる劇的な展開のうち何割かは、単にこうした平均値への回帰によって説明できるかもしれない。だからこそ心身のコンディションを整え「バラつきをなくす」ことや、「バラつきが関係なくなるほどの圧倒的な実力を示す」ことが、スポーツ選手には求められるのだろう。

　ゴルトンとその弟子たちから我々が最も学ぶべきは、バラつきを持つ現象に対する理論的な予測がそれほどうまくいかないという点である。だからこそきちんとデータをとって回帰分析を行ない、その関係性を分析する必要があるのだ。