データ分析における「因果関係の向き」という大問題

統計学の解説書ながら42万部超えの異例のロングセラーとなっている『統計学が最強の学問である』。そのメッセージと知見の重要性は、統計学に支えられるAIが広く使われるようになった今、さらに増しています。そしてこのたび、ついに同書をベースにした『マンガ 統計学が最強の学問である』が発売されました。
第13回では、「因果関係の向き」という統計解析における大問題を紹介します。（本記事は2013年に発行された『統計学が最強の学問である』を一部改変し公開しています。）

因果関係には向きがある

　ここまでに書いたような「比較」および「p値の算出までを含めた解析」を行なえば、きっと意味のあるデータの偏りがすぐに見つけられるだろうし、その偏りをうまくコントロールすれば、効率的に利益をあげられそうなやり方が見えてくるだろう。

　だが、こうした統計解析ができるようになった後、注意しなければいけないのは「因果関係の向き」である。

　たとえば図表15に示すグラフによって「広告の効果」を分析したとしよう。これを見れば、購入者のほうが広告の認知率が高いことがわかる。

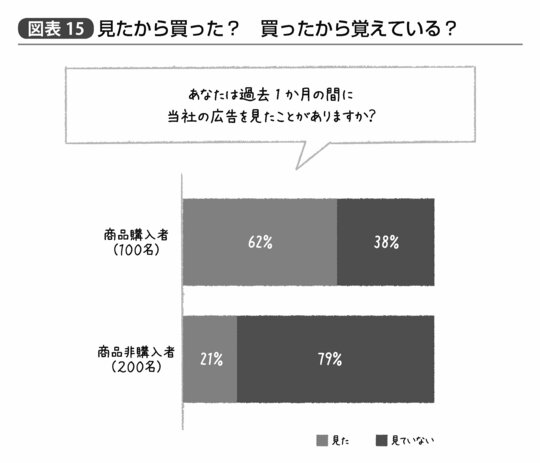
　素直に考えれば、広告を見た人ほど、あるいは同じように広告を見たにせよ広告を後々まで覚えている人ほど、商品を購買している可能性が高いのではないかと解釈するだろう。ちなみにこのような結果のp値、すなわち「本当は何の差もないのに誤差によってこれだけの偏りが偶然生じた確率」は0.1％を下回る。

　しかしながら、このデータと統計解析の結果からは、因果関係の向きとしてはその逆の説明だって成り立つのである。

　すなわち、「広告を認知していたから商品を購入した」のか、「商品を購入したから広告をその後も認知していた」のか、そのどちらの仮説が正しいのかについて、このような一時点の調査データとその解析結果は、p値がいくら小さかろうがまったく情報を与えないのだ。

ゲームと少年犯罪の因果関係は明らかにできるのか？

　こうした問題はしばしば科学的調査においても顕在化する。

　たとえば親に対するアンケート調査の結果、子どもが暴力的なテレビゲームで遊んでいたかどうか、という質問項目と、子どもの犯罪・補導歴の有無の関連性を分析し、少年犯罪者のほうが暴力的なテレビゲームで遊んでいる割合が高かった、という結果が得られたとしても、暴力的なテレビゲームを規制して犯罪率が下げられるかどうかはよくわからないのだ。

　同じようなゲームを遊んでいた子どもたちがいたとして、ある子どもが警察のお世話になったら、その親は「あんな暴力的なゲームをやっていたせいで……」という評価をゲームに対して下すだろう。一方で、大した問題を起こすわけでもなく穏健に育っている子どもの親は、同じゲームを「男の子が好きそうな戦いのゲーム」としか認識しないかもしれない。

　また、同じようなゲームに対して「あんな暴力的なゲーム！」とカリカリする親の子どもは犯罪率が高いという可能性もある。遺伝なのか環境なのかはともかく、同じゲームに目くじら立てるような親とそうでない親の間で子どもの犯罪率が異なる、という可能性は考慮すべきだ。

　さらには、親の感じ方の問題ではなく、実際に暴力的なゲームで遊んでいる時間が長い子どもほどその後の犯罪率が高いという結果が確定したとしても、規制すればそれによって少年犯罪を防止できるかどうかは定かではない。

　なぜならゲームなどからは何の影響も受けないもともとの「暴力性」とでもいった原因があり、この「暴力性」が高い子どもほど暴力的なゲームを好み、また犯罪にも手を染めやすい、といった因果関係が真理かもしれないからだ。この場合、見かけ上少年犯罪者ほど暴力的なゲームのプレー時間は長くなるだろうが、ゲームを規制したからといってその子どもの暴力性が制御できるわけでもない。それでもやはり同じように罪を犯す、ということになってしまう。

「フェア」じゃないからわからない

　ではやはり統計解析は何の役にも立たないのだろうか？

　その答えは「No」である。少年犯罪とゲームのプレー時間に関するデータだろうが、広告認知と購買に関するデータだろうが、既存データから何らかの誤差とは考えにくい偏りを発見すれば、それは貴重な示唆に富む仮説となる。こうした有望な仮説を抽出するスピードと精度こそが現代における統計学の第一の意義であり、うだうだ会議で机上の空論を戦いあわせることなどよりもよほど有益だろう。

　この時点で得られた仮説が単独で価値を生み出すかはもちろんわからない。だが、私たちはここからさらにその仮説が本当に正しいかどうかを実際に検証してみることができる。どのような検証を行なえばどれほどの精度で仮説が確かめられるかわかる、ということも統計学の大きな役割の1つである。

　適切な比較から意味のある違いを発見することで裏ワザが得られると述べたが、一時点のデータから因果関係の向きがわからないというのは、じつはこの比較している集団が同じ条件ではない、つまり「フェアではない」というところに由来している。

　たとえば暴力的なゲームと少年犯罪の関連性を見たいのであれば、「ほかの条件はまったく同じだが、暴力的なゲームのプレーの有無だけが異なっている」という集団同士を比べれば理想的な比較だろう。

　だが実際には、ただアンケート調査を行なっただけでは、この「ほかの条件」がしばしば大きく異なる。暴力的なゲームをプレーする集団とそうでない集団の間では、先ほども述べたように親の性格や考え方などを含む家庭環境も異なるかもしれないし、子どものもともとの心理的傾向なども異なるかもしれないのだ。

2つの解決法

　統計学はこの問題に対して、大きく分けて2つの解決方法を持っている。

　1つは、親の性格なり家庭環境なり本人の心理的傾向なり、「関連しそうな条件」を考えうる限り継続的に追跡調査し、統計学的な手法を用いて、少なくとも測定された条件については「フェアな比較」を行なうというものである。

　そしてもう1つは、解析ではなくそもそものデータの取り方の時点で「フェアに条件を揃える」というやり方である。教育学の分野では、しばしば一卵性双生児を集めて遺伝子の影響を揃えた状態で実験を行なったりするが、そんなことをしないでも「フェアな条件」で実験ができるというのが、次で解説するフィッシャーによる科学哲学自体を揺るがす歴史的大発見である。

　実験というとまるで人間をモルモット扱いしているようで悪いことのように思えるかもしれないが、倫理的に最大限の注意を払いつつ、「本当に正しいやり方は何なのか」を統計学的に明らかにするという取り組みは、経営だろうが医療だろうが教育だろうが、ありとあらゆる分野において世界中で行なわれている。

　適切なやり方で実証実験を行なえば、比較のフェアさは最大限担保することができる。医療における新しい医薬品や治療法も、こうした実証実験抜きに各国政府から認可されることはないと言っていい。現時点で人類がたどり着ける最も正しい真実を知るためには、統計学的に妥当な実証実験が不可欠であるといって間違いないだろう。