【統計リテラシーが格段にアップする】「p値」や「信頼区間」の超本質的な解説

統計学の解説書ながら42万部超えの異例のロングセラーとなっている『統計学が最強の学問である』。そのメッセージと知見の重要性は、統計学に支えられるAIが広く使われるようになった今、さらに増しています。そしてこのたび、ついに同書をベースにした『マンガ 統計学が最強の学問である』が発売されました。本連載は、その刊行を記念して『統計学が最強の学問である』の本文を公開するものです。第20回では、「回帰分析」を非常に有用なツールにした、天才・フィッシャーの偉業について解説します。（本記事は2013年に発行された『統計学が最強の学問である』を一部改変し公開しています。）

ゴルトンの回帰分析の限界

　私が大学時代に受けた実験実習の授業でも「方眼紙上にプロットした点の中心を通る直線を引いてその直線の傾きを読み取りなさい」という100年前に頻繁に用いられたであろう技術の成果をレポートしなければいけなかった記憶があるが、このアナログなやり方に少し数学的な裏付けを与えたのがゴルトンたちの業績である。

　だが逆に言えば、ゴルトンの回帰分析は「データの中心を通る直線とそれを表す数式」を導いただけのものである。だから、たとえば図表20、21の2つのグラフで示す状況を、ゴルトンの回帰分析だけでは区別することができないのだ。

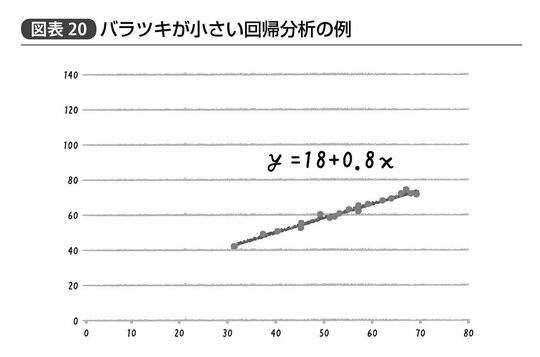
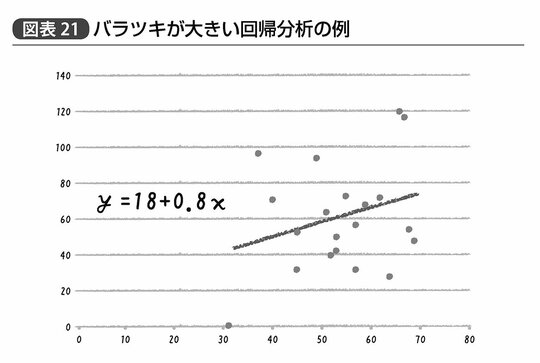
　図表20、21のグラフともに、回帰分析によって得られた中心を通る直線を表す数式、すなわち回帰式はy＝18＋0.8xとなっている。つまりx軸にとった値が1増えればy軸の値が0.8ずつ増える正の関係にあるということだ。なおこの18だとか0.8だとかいう回帰式を表現する数値はそれぞれ回帰係数と呼ばれる。また中学校の数学で習うように、この18を切片、0.8を傾きと呼んでもいい。

　しかしながら、同じ回帰式あるいは回帰係数を持ちながらも、図表20のグラフはあからさまに横軸と縦軸の値が左下から右上へと直線的な関係性を示している一方、図表21のグラフはその関係性が図表20のグラフと比べてそれほどクリアというわけではない。

　どうやら、バラバラな点の中心を通る直線がたまたま見つけられたからといって喜ぶわけにはいかないようである。

　ではこの上下のグラフはどこが違うのだろうか？

　試しに両者のグラフ中に20個ある点からランダムに3つほど取り除いてみたら、と考えてみるといいかもしれない。図表20のグラフは仮にどの3点を取り除かれたとしてもほとんど得られる直線が異なることはないだろう。一方で、図表21のグラフから取り除かれた3点がたまたま最も右上に位置する2点と、左下の1点だったとすると、その中心を通る直線は大きく様変わりすることになる。

　こちらの回帰式はy＝103－0.85xである。つまり、3つの点が失われたことで変数間の関係性が逆転し、xの値が1増えるごとにyは0.85ずつ減少する負の関係となる、ということだ（図表22）。

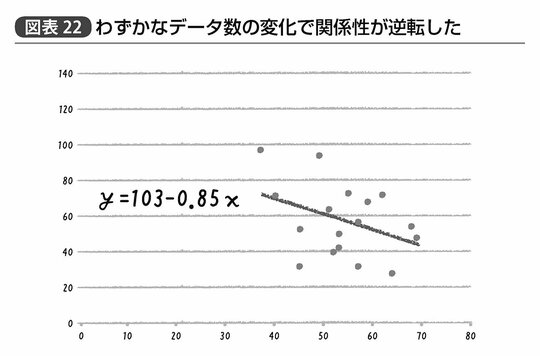
　これではこの回帰分析の結果を利用してyを増加させたいと思っても、xを増やしていいのか減らしていいのかさっぱりわからない。たとえばビジネスの現場で言えば売上（y）を増やしたいと思って広告出稿量（x）の効果を見たいのに、広告を増やしたほがいいのか減らしたほうがいいのか実際にはよくわからない、というのではあまりこの解析に意味はないわけである。

回帰係数自体にバラつきがある

　ここでは20個からランダムな3個を取り除いたら、と考えてみたが、そもそも20個のデータ自体、現実には「自然界から無限に得られるはずのデータからたまたま得られたもの」である。仮に最初から17個のデータを「たまたま」手に入れていたとしたら、先に挙げたような正の関係性を示すかもしれないし、一方で図表22に挙げたような負の関係性を示すことだって考えられる。

　そのため現代的な統計学においては、実際に得られたデータ自体に「比較的大きな値を持つものもいれば小さな値を持つものもいる」というバラつきが存在しているだけでなく、得られた回帰係数自体にバラつきが存在していると考える。すなわち、仮に今後100回「たまたま得られたデータ」から回帰係数を計算したとしたら、「比較的大きな値となることもあれば小さな値となることもある」というバラつきを考慮しなければいけないのだ。

　これは回帰係数に限った話ではなく、データの平均値のように単純なものであろうが、何回もデータを採取して何かしらの値（これを統計量と呼ぶ）を計算すれば、毎回算出される統計量は異なることになるだろう。

　ここで注意しなければいけないのは、たとえばある小学校において4年生のクラス40名全員分の学習データから回帰係数や平均値を算出した場合にも、こうした統計量のバラつきを考えなければいけなくなることもある、ということである。

　確かにニューディール政策の失業率調査とは異なり、全員のデータが得られているからその回帰係数は必ず1つの値に決まる。だからもしこの回帰係数をこのクラス40名の理解のみに使うのであればそこには何の誤差もない。しかしながら、それではせっかくデータを集めて分析した結果は、このクラスの関係者にしか意味を持たないということになってしまう。

　それ以外の人にとっては会ったこともない40名の子どもの成績などどうでもいい。だが、もし彼らと同年代の子どもの成績が何から影響を受けているか、ということがわかるのであれば関心を持つ人はだいぶ増える。つまり、真に知りたい値は「同年代の子どもたち全員」という集団における回帰係数であり、ある小学校のクラス40名というのはたまたまデータの得られた「その一部」ということになる。

　このように考えると、人間が真に知りたいことはたいてい知ろうとする努力が非現実的なものになる場合が多いことがわかる。

　世の中には2、3回失恋したぐらいで「女性はみんな嘘つきだ」と決めつける人もいるかもしれない。もしその発言の真偽を誤差なく確かめようとすれば、30億人ほどの女性全員がウソをつくかを注意深く観察しなければならない。さらに言えば、仮に「2012年時点で女性全員が嘘つきだった」ということがわかったとしても、今後も軽々しく「みんな嘘つきだ」なんて言うことはできない。なぜなら人間の性格や考え方はしばしば変わるものなので、2013年になって嘘つきじゃなくなった女性だっていないとは言えないはずだからだ。

統計学者も理解できなかった「真値」というアイディア

　だが、フィッシャーはこのように「無制限にデータを得ればわかるはずの真に知りたい値」を真値（しんち）と呼び、たまたま得られたデータから計算された統計量がどの程度の誤差で真値を推定しているかを数学的に整理することで、無限にデータを集めることなく適切な判断が下せるという考え方を示した。

　現実のデータから得られた回帰係数などの統計量はあくまでこの真値に対する妥当な推定値であり、単に一番もっともらしい値を推定するだけでなく、それが真値に対してどの程度の誤差を持っているかを考えれば、少なくとも間違った判断を犯すリスクは減らすことができる。

　これこそが、フィッシャーのランダム化比較実験に並ぶもう1つの大きな功績である。

　当時の統計家の誰もが、実際に得られたデータという「具体的なもの」に縛られていた。そこから得られた回帰係数なり平均値なりという値は、先ほど挙げた「40名のクラス全員から得られた結果」のように、絶対的なたった1つの値であると考えていた。だから、抽象的な真値や推定値の誤差というフィッシャーのアイディアについては、意味がよく理解できなかったようだ。だが、それでは先ほど挙げた2枚のグラフの回帰分析の差を解釈することはできないのである。

　与えられたデータから平均値を求める、という計算は小学生でもできる。データを全部足して、データの個数で割ればいい。だが、「算出された平均値は理論上このようなバラつきを持っています」と謎のグラフを見せられたところで、普通は過去の統計学者たちと同様、よく意味がわからないかもしれない。

　だがそうであったとしても、以前に述べた誤差の範囲で説明されるような値の増減に一喜一憂するようなA／Bテストと同様、本来なら無益もしくは有害なことをたまたま得られた回帰係数に基づいて推進するような愚は避けたほうがいい。つまり、傾きの真値が0なのに、得られたデータのバラつきによってたまたま正の回帰係数が得られました、という結果に基づいて戦略を決めるというのは大きな間違いのもととなる。

　広告を増やしても何の意味もない状況で、「回帰分析の結果、広告出稿量を増やせば増やすほど売上があがることがわかったぞ！」と判断していては大損してしまうわけである。

回帰分析を使うための基礎用語

　幸いなことに、そうした抽象的思考が苦手な人であったとしても、現代において統計学は強力なツールとなりうる。数学的なことを理解していなかったとしても推定値や誤差、p値の算出を簡単に行なうためのソフトウェアも普及している。このようなツールから出力される結果について、基本的な意味と読み方さえわかっていれば実用上それほど問題はないだろう。

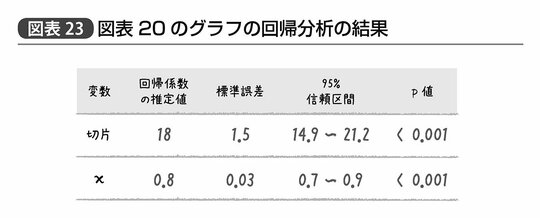
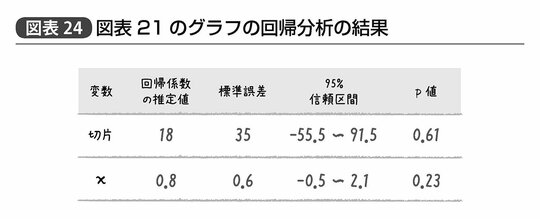
　たとえば、先ほどの図表20、21のグラフの回帰分析の結果を誤差に関する考慮込みで示すと、図表23、24のように示すことができ、それぞれy＝18+0.8xという関係性を示す。

　このとき、図表23、24のそれぞれの項目について次のように解釈すれば、差し当たり間違った判断を犯す愚はだいぶ避けられるだろう。

・回帰係数の推定値：切片・傾き（x）ともにデータから算出された値だがあくまでデータに基づき「真値」を推定した結果だということに注意。

・標準誤差：推定値の誤差の大きさ。回帰係数の推定値と比べて大きければあまり推定値は信頼できないが、この値自体を問題にするよりは後述の信頼区間で考えたほうがいい。

・95％信頼区間：「回帰係数が0」の場合だけでなくさまざまな回帰係数を想定して、「p値が5％以下になる真値としてあり得ない値」とはならない範囲。「ほぼこの範囲内に真値があると考えて間違いない」と考えて大丈夫。

・p値：仮に回帰係数が0だった場合にデータのバラつきのせいだけでこれぐらいの回帰係数が推定されてしまう確率。やはり慣例的には5％を下回ると「さすがに回帰係数0と考えるのはキビシイ」と判断される。

　実際に図表からこのような値を読み取ってみると、たとえば図表23では切片の標準誤差が1.5、xの傾きに関する標準誤差が0.03と、回帰係数の推定値に比べかなり小さい。信頼区間を見てみても、それぞれ14.9～21.2あるいは0.7～0.9という範囲に真値があると考えてほぼ間違いない。

　また、もし仮に回帰係数の真値は0つまりxとyの間に何の関連性もなかったとすると、このような回帰係数がたまたまデータのバラツキによって生じる確率であるp値は、0.001未満つまり0.1％未満ということである。何かしら正の関連性を持っていると考えたほうが妥当だろうというのがここから読みとれる判断だ。

　一方、図表24の回帰係数の誤差を見てみると、切片の標準誤差が35、xの傾きを示す回帰係数については標準誤差が0.6と、回帰係数の推定値とほぼ同じかそれ以上という値が示されている。このときxの傾きについての信頼区間は、マイナス0.5～2.1と「正の値かもしれないし、0かもしれないし、負の値かもしれない」と、まったく要領を得ない。当然p値を見てみても5％以下ということはなく、仮に回帰係数の真値が0であっても切片については61％、xの傾きについては23％程度の確率で、この程度の結果はデータのバラツキによって生じてしまうだろうという結果だ。

　このように、回帰係数の誤差や信頼区間といった値を読み解けるようになれば、あなたの統計リテラシーはぐっとレベルアップする。なぜなら以前述べたようにデータ間の関連性を分析する、あるいはあるデータから何らかの結果を予測する、といった統計学の最も大きな目的のために用いられる手法のほとんどは、広義の回帰分析であるからだ。

　政策・教育・経営・公衆衛生といったありとあらゆる分野の研究結果が、先ほどの図表と同様に、回帰係数とその信頼区間やp値といった（あるいはこの一部を述べる）形で記述されているのだ。