統計学の解説書ながら42万部超えの異例のロングセラーとなっている『統計学が最強の学問である』。そのメッセージと知見の重要性は、統計学に支えられるAIが広く使われるようになった今、さらに増しています。そしてこのたび、ついに同書をベースにした『マンガ 統計学が最強の学問である』が発売されました。本連載は、その刊行を記念して『統計学が最強の学問である』の本文を公開するものです。
第23回では、回帰モデルの限界をカバーするために生み出された「傾向スコア」について解説します。（本記事は2013年に発行された『統計学が最強の学問である』を一部改変し公開しています。）
Photo: Adobe Stock
重回帰分析やロジスティック回帰のような回帰モデルは、データの関連性を見るうえで現在最も頻繁に用いられる便利な手法である。
この「モデル」とは、プラモデルが現実にある自動車や飛行機の「よく表している代替物」をプラスチックで作るのと同様の意味だ。現実にある目に見えない因果関係の「よく表している代替物」を回帰分析によって作るから回帰モデルというわけである。
しかしながら、回帰モデルによって必ず因果関係が適切に推定できるかというと、そういうわけにもいかない。もちろん回帰モデルが無価値なものだなんていうことはないが、どこまでのことが言えてどういった点に注意すべきか、ということがわかってこそ、誤りのないデータの解釈ができるようになる。
ここではそうした回帰モデルの限界と、それを解決するために生みだされた現代的な手法について紹介しよう。
回帰モデルを使う際は交互作用に注意する
重回帰分析では回帰係数の推定について重要な仮定をおいていた。
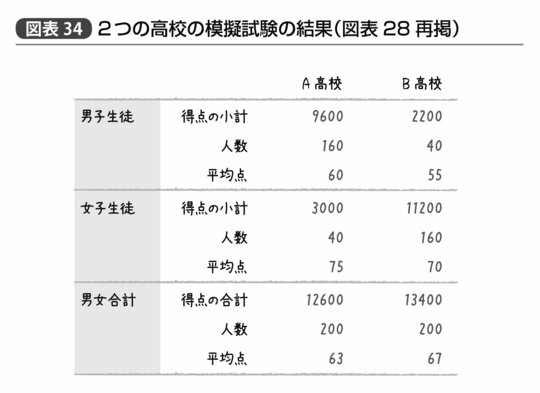
すなわち、回帰係数の推定にあたっては「変数間はお互い相乗効果のない状態で平均的にどういった違いが生じているか」を考えたというものだ。図で説明するにあたって用いた数値もわかりやすくするために、A高校だろうがB高校だろうがどちらにおいても男女間の平均点の差は「ちょうど15点」で、男子も女子もA高校の生徒はB高校に比べそれぞれ「ちょうど5点」高かった（図表34）。
だが実際には、ここまで「ちょうど」ということはない。たとえば図表35のようになった場合はどうだろう。
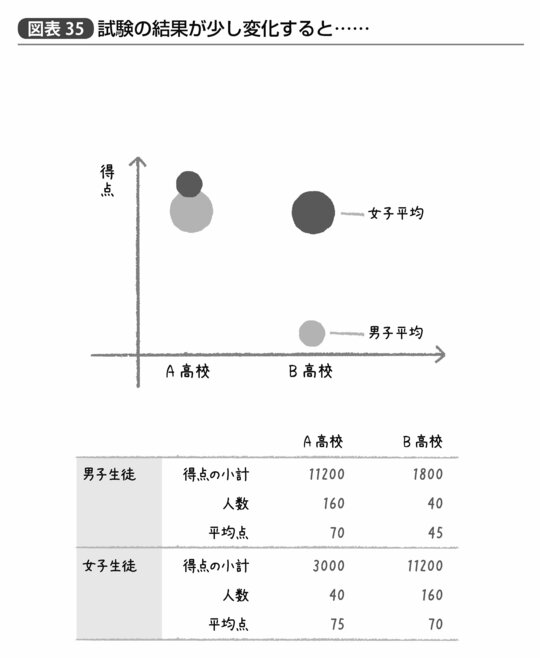
A高校における5点の差とB高校における25点の差を単純平均するならば、確かに全体的に女子は男子と比べて15点ほど成績がいい。
だが、実際にはB高校の男子のみが異常に成績が悪い一方、その例外的な層を除くと男女間の差も高校間の差もそれほど見られない、という状況である。これが「お互いに相乗効果のない状態」だという仮定が崩れているということだ。もし相乗効果がない状態であれば、A高校においてもB高校においても同じように男女間の差が見られ、また男女それぞれで同じように高校間の違いが見られたはずなのだ。
なお、この相乗効果のことを英語ではインタラクションと呼び、統計学的な訳語として交互作用という言葉が与えられている。
回帰モデルを使ううえで重要な注意点の1つが、このような交互作用が本当に存在していないかというものである。しかし実際に交互作用が疑われるのであれば、それも回帰モデルに含めて回帰係数を推定してやることはできる。
つまり、それぞれが連続値だろうが、ダミー変数だろうが、2つの説明変数それぞれの回帰係数だけでなく、2つの変数を掛けあわせた新しい説明変数（これを交互作用項と呼ぶ）を作り、その回帰係数についても同時に推定する、というだけでこの交互作用の影響は推定することができるのである。
試しにまとめるとしたら図表36のような形になるだろう。
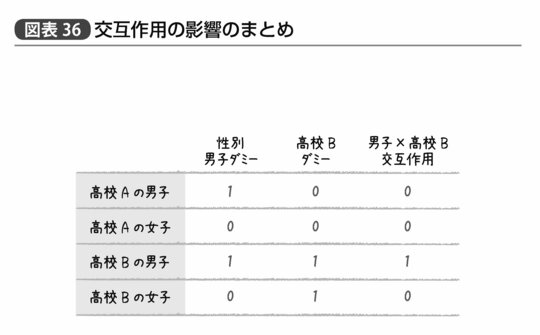
この交互作用が1か0か、というのは、つまり「B高校かつ男子」か「それ以外」かということだ。これは、男女間で平均的な違いがあり、高校間で平均的な違いがあるというだけで説明できない「特にB高校の男子に違いが見られる」という影響を表す。なおダミー変数のつけ方によって「A高校かつ女子」という交互作用項を設定しても推定上まったくかまわないのだが、重要なのは、この交互作用項を導入したことによって、2つの高校×2つの性別の組み合わせで生じる全部で4つのグループ間の平均値の差がすべて回帰係数によって表現できるという点である（図表37）。
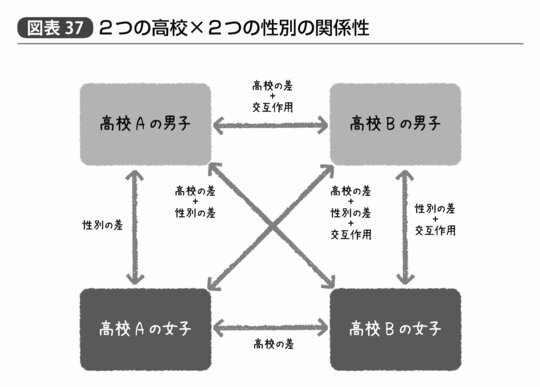
このように交互作用項を含めた回帰モデルを作ってやれば、見かけ上の回帰係数によって誤った判断を下すリスクは下げられるだろう。
ドツボにはまる変数選択作業
しかしながらその一方で、正確さを求めるあまりすべての交互作用項を検討していたら、わけのわからない結果になってしまうという問題もある。
元の説明変数が2つで、その間の交互作用項1つを加えるぐらいであれば問題がないが、もし仮に説明変数が20個あれば、その間の交互作用項は20×19÷2＝190もの数になるのである。
サンプルサイズが限られている状況でこのように大量の回帰係数の推定を行なえば誤差は大きくなるし、仮に「ビッグデータ」ゆえにサンプルサイズが無制限に確保できたとしても、100を超える数の回帰係数をすんなり解釈できるほど人間の認知機能は優れていない。
「みんな違ってみんないい」というのは人と接するうえではとてもよい言葉だが、データを分析して結局わかったのが「みんなそれぞれ違う」というのでは話にならないのだ。可能な限りシンプルに、「何が最も結果変数に違いを生むのか」がわかってこその統計学である。
そのため、交互作用項も含め自動的に誤差とは考えにくい説明変数だけを選び出して回帰モデルを構築する変数選択法と呼ばれるアルゴリズムも研究されている。また、どのような説明変数あるいは交互作用項を含んだ回帰モデルが一番データの当てはまりとして適当かを判断するための指標もいくつか開発されている。たとえばその中で最も代表的なものの1つに、元統計数理研究所所長の赤池弘次が1973年に発表した赤池情報量規準（AIC：Akaike's Information Criterion）と呼ばれる指標がある。
しかしながら、実際にどのような回帰モデルが妥当か、というのは数理的な性質だけで決定を下してよい問題ではない。
適切な変数を選択し、調整すべき条件がすべて正しく考慮されていれば、回帰モデルによって「フェアな比較」を行なうことができることは間違いない。だが、何をもって適切なモデルが得られたとするかという点については、統計家だけでなくその結果に関わるステークホルダーたちによって慎重な議論を経なければいけないのだ。
限りなくランダム化に近づく「傾向スコア」
このような問題に対して有効な解決策が1983年に提案されている。
それはローゼンバウムとルービンという統計学者によって発表された傾向スコアあるいはプロペンシティスコアと呼ばれる手法である。この方法は主に疫学分野でランダム化が不可能あるいは困難な因果関係の特定に重宝されてきた。
傾向スコアとは、興味のある二値の説明変数について「どちらに該当するか」という確率のことを言う。「どちらに該当するか」という傾向を示す値だから傾向スコアというわけである。なお傾向スコア自体は、すでに紹介したロジスティック回帰によって簡単に得ることができる。
たとえば喫煙するかどうかという行動が、肺がんという結果の原因になっているかどうか、という因果関係はその実証がむずかしいという話を第17回に書いた。タバコを吸わせるか吸わせないか、というランダム化比較実験ができれば、喫煙の有無以外の条件はすべて平均的に等しいグループの間で肺がん発生率のフェアな比較ができるのだが、そうした研究は倫理的に許されない。
そのため「同じ条件の対象者を集める」といったやり方が考案されてきたが、考慮すべき条件が増えると大量のデータが必要になる。また先ほど説明した変数選択のドツボも問題になりうるだろう。
ルービンとローゼンバウムが発見したのは、傾向スコアが同様の集団、つまり年齢や居住地域、職業などの条件から推定された「喫煙するだろう」という確率が同じ集団同士で比較すれば、「その他の条件」と「喫煙の有無」の関連性が「喫煙の有無」と「肺がん」の関連性を歪めることはなくなるということだ。
仮に女性より男性の喫煙率が高く、都会の住民よりも地方の住民の人の喫煙率が高かったとしよう。また、女性よりも男性のほうが、都会の人よりも地方の人のほうが肺がんにかかりやすかったとする。この場合、喫煙自体には何の影響がなくても、データの偏りのせいで見た目上肺がんになりやすくなるというシンプソンのパラドックスが問題になる。
だが、これはさまざまな条件の違いによって喫煙率が左右されるから起こる問題である。逆に言えば性別や居住地域などの諸条件から推定される喫煙率が同じ集団同士に絞ってしまえば、そうした諸条件が喫煙率に影響することはない。つまり、少なくとも喫煙率の推定に用いた条件に関しては、ランダム化比較実験と同様のフェアな比較ができるということである。
同じ傾向スコアによって層別に比較を行なうとはすなわち、「他の条件で言うとタバコを吸わないはずなのになぜかタバコを吸っている人」と「他の条件で言うとタバコを吸わないはずだしやっぱりタバコを吸わない人」の比較を行なっている、と考えればフェアな比較を行なっているイメージがつきやすいかもしれない。
傾向スコアは簡単に限りなくランダム化に近い因果関係の推定が行なえることから、今や疫学だけでなく政策や教育の評価にもよく使われるようになっている。80年代から90年代にかけて傾向スコアを応用する手法の洗練もずいぶんと進んだ。もちろんランダム化とは違い「未知の大きく結果を歪める何か」を完全に取り除けたとは言い切れないが、だからといって細かい厳密さにこだわるあまり判断を保留し続けることが常に賢明とも言えない。
人類はすでに因果関係を把握しコントロールする術を手に入れている。怪しげな霊媒師に頼るまでもなく、ちょっと勉強してデータをいじりさえすれば最善の判断は下せる。あとはもう、この知恵を使っていかに価値を生み出すか、というだけの話なのだ。
▶『マンガ 統計学が最強の学問である』の刊行に寄せて
『マンガ統計学が最強の学問である』は、言語化・定型化された仕事がAIに奪われていくなかで、「新たに何をするか考えて決める」スキルを日本に最大限広げるために制作されました。
実は初代『統計学が最強の学問である』はほとんど数式を使わず、統計学がどう生まれてどう役に立てられるのかにフォーカスした、統計学の本としては少し変わった本でした。しかし、40万部以上売れただけあって、あの本を読んで統計学を面白いと感じ、本格的に勉強しようとしたり、実務に活かすようになった、という方と私は日々の仕事の場で頻繁にお会いします。統計手法の数理面を細かく説明したり、統計解析をおこなうためのプログラミングに関する本は多数ありますが、それはちょうどAIのサポートが手厚くなっている部分です。今の時代はそれよりも、「統計学を活用したい」というモチベーション、「どのような課題に対して統計学を活用するか」という課題設定のコツ、そして分析結果の読み解き方と、結果を踏まえて何をやるべきかを考える枠組みといったスキルのほうが相対的に重要になってきているのではないでしょうか。
本書が目指すのは、まさにそうした今こそ必要な「統計学の活かし方」を、物語を通して皆さんにお伝えすることです。たとえば『SLAM DUNK』というマンガを読むことでバスケットボールをプレイするモチベーションが喚起されたり、バスケットボールの観方がわかるようになったりといった方がたくさんいるように、すばらしいマンガは多くの人の人生を変える力を持っています。ありがたいことに私にとっても大好きな漫画家であるうめさん（小沢高広さんと妹尾朝子さん）に漫画制作を依頼できたことで、ストーリー面でも作画面でもすばらしいものになりました。私自身のデータ活用に関わる経験を凝縮した物語を、うまく追体験していただければ幸いです。
また各話の最後には、それまでに出てきた統計手法について、できる限りわかりやすく、かつ簡潔に説明した解説を加えました。ストーリー内ではあまり説明臭くならないよう、しかし気になるであろう知識面はその後の解説で補足できるよう個人的にバランスをとったつもりです。
本書をきっかけに、さらに多くの人が統計学を学び、「新たに何をするか考えて決める仕事」をする力を手にしていただければ幸いです。
