統計学の解説書ながら42万部超えの異例のロングセラーとなっている『統計学が最強の学問である』。そのメッセージと知見の重要性は、統計学に支えられるAIが広く使われるようになった今、さらに増しています。そしてこのたび、ついに同書をベースにした『マンガ 統計学が最強の学問である』が発売されました。本連載は、その刊行を記念して『統計学が最強の学問である』の本文を公開するものです。
第22回では、「重回帰分析」とそれを拡張した「ロジスティック回帰」について解説します。（本記事は2013年に発行された『統計学が最強の学問である』を一部改変し公開しています。）
Photo: Adobe Stock
学者も多用する統計手法の主役
一般化線形モデルという枠組みによって、データ間の関連性を分析したり推測を行なったりする解析のほとんどは、広義の回帰分析の一部であると整理することができた。
このうち重回帰分析は、説明変数すなわち予測したい結果に影響する要因が複数ある状況へ拡張された回帰分析であるが（図表25）、これも統計学において重要な「フェアな比較」を行なううえで重要な役割を果たす統計解析手法である。
そのため政府のレポートにおいても学者の論文においても、何らかのデータ分析を行なうもののほとんどは、重回帰分析やその拡張であるロジスティック回帰の結果が示されている。現代における統計手法の王道あるいは主役と言ってもよいかもしれない。これらの手法さえ理解し、読み解けるようになれば、あなたは学者たちとも対等に議論できるようになるだろう。
では、なぜ重回帰分析やロジスティック回帰によって「フェアな比較」を行なうことができるのだろうか。
フェアな比較が崩れるシンプソンのパラドックス
「フェアな比較」ができないことによってデータからの判断を誤りうる例の1つに、シンプソンのパラドックスと呼ばれるものがある。シンプソンとはこの問題の最初の提唱者だ。
たとえば次のような問題を出された場合、あなたはどう答えるだろう？
A高校とB高校の同じ学年の生徒に対して同じ模擬試験を受験させた。
男子生徒同士で比べるとA高校の平均点はB高校よりも5点高い。
女子生徒同士で比べるとA高校の平均点はB高校よりも5点高い。
ではA高校とB高校の平均点を男女全体で比較するとどちらが高いだろう？
普通に論理的な思考を働かせれば、当然のようにA高校のほうが5点分平均点は高いと考えられる。だがここで「必ずしもそうとは限らない」と考えられるかどうかが統計リテラシーの力である。そうとは限らない状況の一例を具体的な数値で示すとすれば、図表28のような場合が該当するだろう。
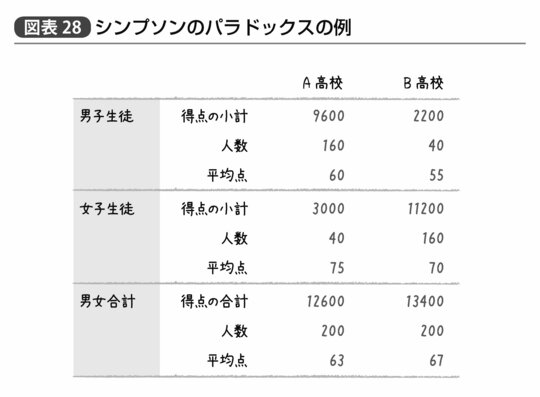
図表28のような状況において、A高校の男子全員の得点を合計すると9600点となり、これを160名という人数で割ると60点になる。また女子生徒の得点の合計は3000点でこれを40名という人数で割ると75点になる。ゆえにA高校の男女合わせた全学年での平均点は（9600+3000）÷（160+40）で63点となる。一方で、同様の計算から得られるB高校の全学年での平均点は67点である。
確かに表のそれぞれを見ると、A高校の男子平均点が60点に対しB高校では55点、A高校の女子平均点が75点に対しB高校では70点と、先ほど出した問題文との矛盾はない。だが男子と女子の平均点に差があり、またA高校とB高校の生徒の男女比が異なっているために、全校での平均点はB高校のほうが4点高くなってしまっているのだ。
このように、全集団同士での単純比較は、その内訳となる小集団同士との比較の結果と矛盾することもある、というのがシンプソンの指摘である。ランダム化を行なっていない疫学などの観察研究において、単純な比較で一見大きな差が生まれたとしても、それは単にA高校とB高校の男女比と同様の「内訳」の違いかもしれない。逆に、単純な比較ではまったく差が見られなくなってしまっているのも、やはり「内訳」の違いによって本来あるべき差が隠されているだけかもしれない。
たとえば以前紹介した「暴力的なゲームのプレーと少年犯罪率」という因果関係の分析を思い出してほしい。家庭環境という「内訳」を揃えて比較すれば何の差もないのに、暴力的なゲームをプレーするグループのほうに家庭環境の悪い子どもがより多く含まれていれば、見かけ上は暴力的なゲームのプレイヤーのほうが犯罪率が高いということになってしまう。
層別解析でパラドックスは防げるが……
だから疫学のような観察研究では条件を揃える必要があった。A高校とB高校の成績を男女別に見るように、あるいは家庭環境別にゲームのプレーの有無と犯罪率を見るように、結果に影響しうるような条件について「同様の小集団」同士で比較すれば、シンプソンのパラドックスはほぼ避けられるはずだ。なお「同様の小集団」つまり「層」ごとに区切って分析を行なうことを層別解析と呼ぶ。
この考え方は基本的に正しい。だが、「結果に影響しうるような条件」が多くなれば、このようなやり方は徐々にうまくいかなくなってくるのである。
考慮すべき条件が増えてくると、層別解析がうまくいかなくなる理由について理解するために、A高校とB高校の成績比較において、生徒の性別以外にも考慮すべき条件がないか検討してみよう。
たとえば、①部活動が運動部か文化部か帰宅部か、②塾に通っているかどうか、③さらに家庭環境を示すものとして親の年収を3カテゴリーに区分して考慮することにしたとすると、これらの条件がすべて同様となる小集団すなわち層はいくつ考えなければならないだろうか。
答えは以下の通りだ。
2（性別）× 3（部活動）× 2（塾の有無）× 3（親の年収）＝ 36
すなわちこれらすべての条件において「同様」と考えられる層を作るとすれば、36個の層を作らなければいけないのである。
では各学校に、それぞれの層に該当する生徒はいったい何人いるだろうか？ どの条件についても均等に分かれたと仮定してもで層あたり5、6人しか該当しない。しかも男女比はどちらの高校でも偏っているので、たとえばA高校にいる40人の女子生徒を性別以外の条件で均等に18層に分けると、平均して層あたり2、3人しか該当しない。これほど少人数では、どんな分析をしようがどんな結果が生じようが、誤差の範囲としかならない。
層分けを不要にする重回帰分析
こうした問題に対して重回帰分析は威力を発揮する。「性別によって点数は異なるから同じ条件にしよう」というやり方から考え方を一歩進めて、「性別によって点数が平均的に何点異なるのか」を推定すれば、層別に分けなくてもよくなるのである。以下でこの考え方を詳しく見ていこう。
仮に性別を考慮せずにA高校とB高校の間で平均点の比較をしたとすれば、図表29のような回帰分析を行なっていることになる。このことは前回の内容を踏まえればわかるだろう。
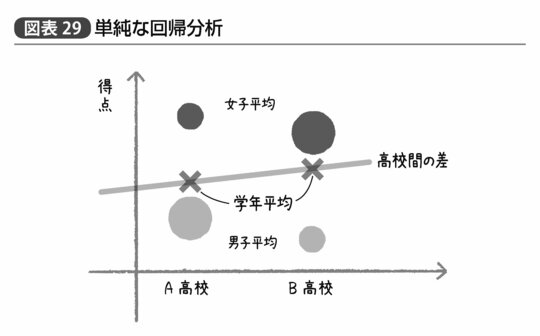
薄い丸が男子の平均点で濃い丸が女子の平均点、丸の大きさはそれぞれ生徒の人数を示しており、×で示すような高校ごとの単純な平均点（それぞれの学校で人数が多いほうの性別よりになる）を通る直線の傾きが「高校間の平均点の差」だ。この場合、傾きは右上がりとなっており、BのほうがAよりも平均点が高いという結果になっている。
だが、性別の違いを推定したらどうなるだろう？ つまり、A高校でもB高校でも女子の平均点は15点高い、という情報を使うのだ。
この情報に基づいて、高校間で性別に関する「フェアな比較」をしようと思えば、「仮にそれぞれの高校の男子生徒が全員女子だったら」とでも考えてみればいい（図表30）。
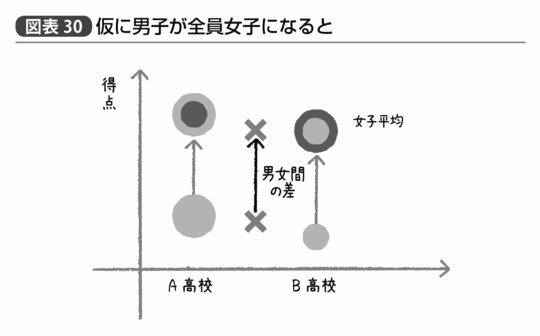
そうすると、どちらの高校についても男子全員の値に対して15点を足すことになり、A高校の平均点は75点、一方B高校の平均点は70点ということになるだろう。つまりシンプソンのパラドックスは回避され、「A高校のほうが平均点が5点高い」という直感通りの結果が得られるのである（図表31）。
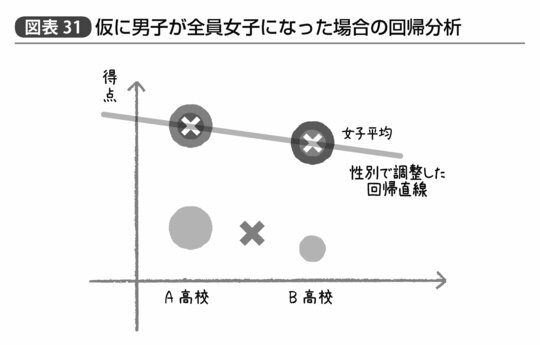
このように、性別の違いにより平均で何点違うか、という回帰係数と、高校によって平均で何点違うか、という複数の回帰係数を同時に推定するのが重回帰分析である。性別の違いによって「平均で何点違うか」という影響の度合いが推定できれば、男子同士・女子同士という層別で比較しなくても、「もし仮にこの男子が全員女子だったら」と仮想的に条件を揃えた状態でフェアな比較をしていることになるのだ。
これが重回帰分析によってフェアな比較が行なわれたということである。こうしたやり方であれば、多少条件が増えたとしても莫大な数の層に分ける必要はない。
複数の回帰係数は「お互いに相乗効果がなかったとすれば」という仮定のもと、説明変数が結果変数にどの程度の影響を与えるかを示している。このことさえ読み取れるようになれば、みなさんはもう学者の論文や国の政策レポートすら誰の助けも借りずに理解することができるのだ。
たとえばオックスフォード大学教授である苅谷剛彦が著した『学力と階層』という本の中には、1989年と2001年に大阪府下の小中学校を対象にした、生活・学習習慣と成績の調査データを重回帰分析した結果が示されている。
その詳細については同書を実際に目を通してもらうとして、たとえば2001年の中学生の数学の正答率（すなわち100点満点での点数）に関して図表32のような重回帰分析の結果が得られた、と言われれば、その意味することはもう明らかだろう。
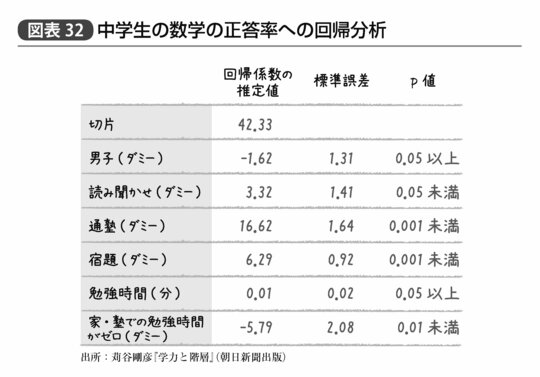
信頼区間が示されておらず、またp値が実際の数値ではなく、0.001未満／0.01未満／0.05未満／0.05以上という分類で示されているのがこれまでに例示したものと異なっているが、それでもこの表からは、「男子のほうが女子より1.62点低い」「家庭で読み聞かせをされたことのある生徒は3.32点高い」「通塾しているものは16.62点高い」「宿題をきちんとやる者は6.29点高い」「家庭や塾での勉強時間の長短による成績の影響は誤差と言える範囲」「だがゼロかどうかは誤差の範囲を越えて5.79点分の悪影響」ということが読み取れるはずだ。
また、この中でも特に影響の大きい要因は塾通いの有無である。宿題を真面目にやって長時間家庭で勉強する子どもよりも、学校の宿題をやらず塾通いだけをする子どものほうが理論上よい成績を取る、というのでは学校の学習指導がうまくいっているとは言えず、また塾通いをさせられるかどうかという家庭環境が成績に大きく影響するというのは、社会的な不公平を示しているかもしれない。重回帰分析のことがわかれば、こうしたことが直感などではなくきちんとしたデータから議論ができるようになるのである。
オッズ比を用いるロジスティック回帰
重回帰分析は結果変数が連続値である場合にしか使うことはできないが、フラミンガム研究において、それをさらに拡張したロジスティック回帰というものが発明されている。
心臓病になるかどうか、という二値の結果変数に対して、重回帰分析と同様にさまざまな説明変数（血圧や年齢、喫煙の有無など）が与える影響をフェアに分析しようと、この手法は生みだされた。
数学的な部分については専門書などを参照してもらうことにしてここでは説明を省くが、もともと0か1かという二値の結果変数を変換し、連続的な変数として扱うことで重回帰分析を行なえるようにした、というのがロジスティック回帰の大まかな考え方である。
ロジスティック回帰では、回帰係数をオッズ比つまり「約何倍そうなりやすいか」で示すということさえ知っていれば、結果の理解に問題はないだろう（なお正確には、推定された対数オッズ比を変換しオッズ比の形で結果を示す）。重回帰分析と同様に、回帰係数の推定値、標準誤差と信頼区間、それにp値というのが読み取るべき値であり、その回帰係数の結果の読み方だけが少し異なるのだ。
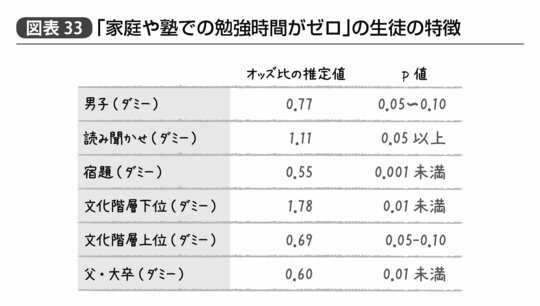
先ほどの『学力と階層』には、「家庭や塾での勉強時間がゼロ」になる生徒の特徴についてのロジスティック回帰による分析も行なわれているので、その結果のオッズ比とp値も紹介しよう。
こちらについては男子かどうか、読み聞かせをしたことがあるか、家庭の文化階層が上位グループかというのは「誤差の範囲」であるが、宿題をきちんとしているものが「勉強時間がゼロ」になる割合は0.55倍とほぼ半減（この点はどちらが原因でどちらが結果かという解釈はむずかしいが）、また家庭の階層が下位グループであれば「勉強時間がゼロ」になる割合が1.78倍、父親が大卒であれば0.60倍と塾通いの有無以外にも家庭環境による学習習慣の影響は大きいのではないかという結果が示唆されている（図表33）。
回帰分析が読めれば「いいかげんな言説」が駆逐できる
社会問題に関する提起であれ、ビジネスの改善に関する言説であれ、ここまでの統計リテラシーが身につけば、何のデータもなしにいいかげんなことを言う人にだまされることはなくなるはずだ。
私は意地が悪いので、テレビやネットで学者や文化人がいいかげんなことを言うたびに、その出典となりそうなデータを探してみることにしているのだが、思った以上に世の中には何の根拠もなくいいかげんなことを述べる人が多い。
何か「いいかげんな言説」に疑問を持った際には、その疑問を持ったトピックと回帰分析という単語でGoogle検索をしてみるだけでも、「何の要因が関連しているのか・関連していないか」という結果を探すことはできるはずだ。ぜひここまで培った統計リテラシーを活かして、いいかげんな言説を駆逐してみてほしい。
▶『マンガ 統計学が最強の学問である』の刊行に寄せて
『マンガ統計学が最強の学問である』は、言語化・定型化された仕事がAIに奪われていくなかで、「新たに何をするか考えて決める」スキルを日本に最大限広げるために制作されました。
実は初代『統計学が最強の学問である』はほとんど数式を使わず、統計学がどう生まれてどう役に立てられるのかにフォーカスした、統計学の本としては少し変わった本でした。しかし、40万部以上売れただけあって、あの本を読んで統計学を面白いと感じ、本格的に勉強しようとしたり、実務に活かすようになった、という方と私は日々の仕事の場で頻繁にお会いします。統計手法の数理面を細かく説明したり、統計解析をおこなうためのプログラミングに関する本は多数ありますが、それはちょうどAIのサポートが手厚くなっている部分です。今の時代はそれよりも、「統計学を活用したい」というモチベーション、「どのような課題に対して統計学を活用するか」という課題設定のコツ、そして分析結果の読み解き方と、結果を踏まえて何をやるべきかを考える枠組みといったスキルのほうが相対的に重要になってきているのではないでしょうか。
本書が目指すのは、まさにそうした今こそ必要な「統計学の活かし方」を、物語を通して皆さんにお伝えすることです。たとえば『SLAM DUNK』というマンガを読むことでバスケットボールをプレイするモチベーションが喚起されたり、バスケットボールの観方がわかるようになったりといった方がたくさんいるように、すばらしいマンガは多くの人の人生を変える力を持っています。ありがたいことに私にとっても大好きな漫画家であるうめさん（小沢高広さんと妹尾朝子さん）に漫画制作を依頼できたことで、ストーリー面でも作画面でもすばらしいものになりました。私自身のデータ活用に関わる経験を凝縮した物語を、うまく追体験していただければ幸いです。
また各話の最後には、それまでに出てきた統計手法について、できる限りわかりやすく、かつ簡潔に説明した解説を加えました。ストーリー内ではあまり説明臭くならないよう、しかし気になるであろう知識面はその後の解説で補足できるよう個人的にバランスをとったつもりです。
本書をきっかけに、さらに多くの人が統計学を学び、「新たに何をするか考えて決める仕事」をする力を手にしていただければ幸いです。
