「ミシンを2台買ったら1割引き」で売上は上がるのか？――「攻め」のための統計学

統計学の解説書ながら42万部超えの異例のロングセラーとなっている『統計学が最強の学問である』。そのメッセージと知見の重要性は、統計学に支えられるAIが広く使われるようになった今、さらに増しています。そしてこのたび、ついに同書をベースにした『マンガ 統計学が最強の学問である』が発売されました。第16回では、「攻め」の姿勢をとるにあたっても、ランダム化比較実験がどれほど大きな意義を持つかについて解説します。（本記事は2013年に発行された『統計学が最強の学問である』を一部改変し公開しています。）

「攻め」のための統計学

　過ちを避けるための「守り」のランダム化比較実験の意義がわかったら、今度は「攻め」の姿勢をとるにあたっても、ランダム化比較実験がどれほど大きな意義を持つかについても考えてみよう。

　ランダム化比較実験は過ちを犯す可能性を小さなコストとリスクでつぶすことができる。これを逆に言えば、小さなコストとリスクで「あえて間違いを犯すこともできる」ということになることがおわかりいただけるだろうか。

　あるいは「あえてバカな思いつきを試す」と言い換えてもいいかもしれない。たとえばあなたが裁縫や編み物などのホビーグッズを通販する会社に勤めていたとして、部下や後輩が「ミシンを2台買ったら1割引きっていうキャンペーンはどうですかね？」というアイディアを提案してきたらどうするだろうか？

　ミシンなんて普通一家に1台あれば事足りる物である。仮に裁縫を趣味にする女性が2名以上いる大家族だって、わざわざミシンを取り合うことはないだろう。まっとうな感覚を持った大人の多くは、「こいつは何をバカなことを言ってるのか」と一笑に付してしまうのではないだろうか。

　だが、これはわざわざ私が考えた「バカな思いつきのたとえ話」ではない。それどころかこの「バカな思いつき」は、実在するアメリカの企業において顧客1人あたりの売上高を3倍以上に増加させた、とんでもない大成功キャンペーンのもとになったのである。

「誤り」と決めつけることの愚かさ

　ジョーアンファブリック社は元来細々と布地を売るだけの会社だったが、この種の企業としては早い段階からインターネット通販に進出し、今では裁縫や編み物、ケーキデコレーションなど家庭的なホビーに関する総合企業として大きく成長した。日本で言えば「ユザワヤがネット通販で成功した感じ」と考えてもらえれば、それほど間違いではないと思う。

　彼らは月に100万件以上のユニークアクセスを生かし、積極的なA／Bテストに取り組んでいた。何かしらのプロモーションキャンペーンを打つときはいつも複数の案をランダム化して試せるのだから、会議でごちゃごちゃと考えるより、「とりあえず試してダメそうならやめよう」と考えたほうが遥かに合理的である。「害はないけど意味もなさそう」程度のアイディアだったら、ランダム化する本命プランの比較対照に含めておいてもそれほど大きな損はない。

　そうして彼らが少しずつ大胆な「攻め」の姿勢を見せていたところでつかんだ大成功が、先ほどの「ミシンを2台買うと1割引き」というキャンペーンだったのだ。

　その結果現実に起こったことは、シンプルだが我々が想像もしなかったような現象である。このキャンペーンを目にした顧客たちはもちろん2台のミシンを欲しがっていたわけではなかった。だが、ほしいミシンが1割引きになるのなら、と、わざわざ隣人や友人を誘って共同購入を呼びかけたのである。

　すなわち、ジョーアン社は思いもよらず、優秀なセールススタッフたちを雇い入れることができたのだ。その結果、先ほども言ったように、このキャンペーン広告が表示された顧客グループは、そうでなかった顧客グループに比べ平均して1人あたり3倍以上の売上を示したのである。

　もちろんこの両者はランダム化の結果、表示された広告以外は平均的に等しい集団であると考えられる。だから、この3倍以上という売上の差の原因は、「どのキャンペーン広告が表示されたか」という要因によってもたらされたと考えてほぼ間違いはない。

　もしあなたの企業が過剰に失敗を恐れ、新しいアイディアを提案することよりも、それをもっともらしい理由で否定することのほうを賞賛するような体質になっていたとしたら、それはとてももったいないことである。ムダなリスクやコストを避けることはもちろん重要だが、統計学的な裏付けもないのにそれが絶対正しいと決めつけることと同じくらい、統計学的な裏付けもないのにそれが絶対誤りだと決めつけることも愚かである。

　きちんとした統計学的思考ができている限り、ビジネスにおけるランダム化比較実験のコストは近年ではそれほど高いものではない。たとえば複数のDMデザインのうちどれがよいか、というような、いくら話し合っても確実な正解が出せるわけでもない議題には仕事上いくらでも出くわす。だが、人件費を浪費して終わりのない会議を繰り返すよりは、比較的安価な媒体で小規模なランダム化比較実験を行なったほうが、早く、安く、確実な答えを得られる可能性が高いのである。

1億5000万ドルを稼いだクレーム対応

　ランダム化比較実験が意義を発揮するのは、何もマーケティングの領域に限った話ではない。顧客への対応にしても、社内人事にしても、全社的な正解のない判断を個人のセンスに任せるぐらいなら、とりあえずランダム化して定期的に評価する、というやり方のほうが長期的なメリットは大きいだろう。

　たとえばコンチネンタル航空では、飛行機が遅延したりダブルブッキングでキャンセルさせられたときのアフターケアをどうするか、という問題に対してランダム化比較実験を行なったことがあるそうだ。

　彼らはこうしたトラブルが起きた客をランダムに3グループに分けた。①「ただ正式な謝罪のレターを送る」か、②「謝罪レターに加えプレミアムクラブへのお試し無料入会期間を与える」か、そして比較対照として③「特に何もしない」というのがその内訳だ。

　その後の調査の結果、詫び状のなかった人たちは何ヵ月か経った後でもまだ怒っていた。一方で、詫び状を受け取った2グループは翌年コンチネンタル航空へ費やすお金が8％も増えていたらしい。つまり、「嫌な思いもしたけどなかなかよいやつらじゃないか」と、逆に彼らはコンチネンタル航空が好きになったのだ。さらにはプレミアムクラブ無料入会期間を与えてもらった顧客の3割ほどは、無料期間が終わった後も自腹で会費を払い、コンチネンタル航空はさらに追加の収入を得ている。

　もちろん彼らは、その後トラブルが起こる度に、せっせと詫び状とプレミアムクラブへの案内を送るようになった。その結果、1億5000万ドル以上の売上増加が得られたそうだ。

　社内のありとあらゆる「正解のない意思決定」について、正解がないのであればとりあえずランダムに決めてしまう、という選択肢の価値はもっと認められるべきだろう。ただ決定をランダムにすることと継続的にデータを採取することさえ心がければ、後で正確に「それがよかったのか」「どれぐらいの利益に繋がったのか」が評価できるのだから、少なくともそちらのほうがより確実に「正しい判断」へと近づく道になることもある。

ランダムは意外とむずかしい

 　ちなみにランダムというと「デタラメ」「いい加減」と解釈されることもあるが、少し意味は異なる。「無作為」という訳が与えられることもあるが、要するに人間の意思がそこに入り込まないようにすることだ。あるいは「確率的」と言うこともできるだろう。

　ここで注意しなければいけないのは、人間が「無作為らしく」あるいは「テキトーに」出した数字は、しばしばそれほどランダムではなかったりするという点だ。

　択一式の試験問題の正解を何にするか、出題者は「テキトーに」決めているはずだが、なぜかAが正解である確率よりも、Cが正解である確率のほうが偶然とは考えにくいレベルで高かったりする。

　また、Aという文字とBという文字をランダムに3つ並べると、「AAA」もしくは「BBB」という同じ文字が3連続するのは8パターン中2つ（25％）もある（図表17）。

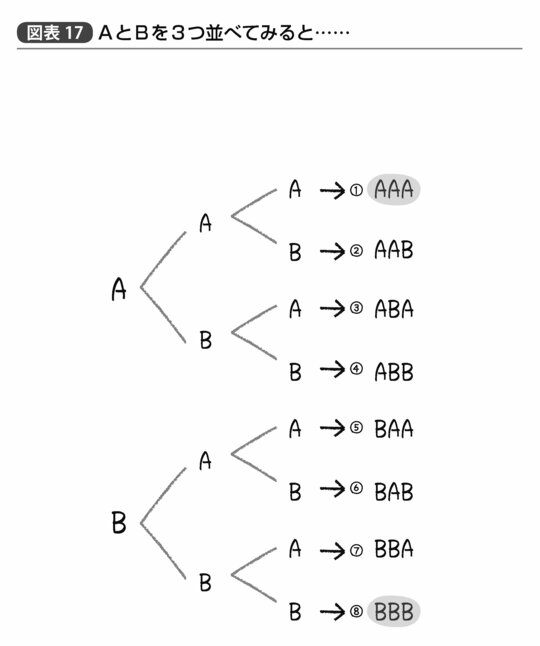
　一方で、Aという文字とBという文字を「3つテキトーに」並べてくださいというと、人間はしばしば「3文字続くと不自然かな？」と、よくわからない配慮でこのパターンを避けがちだ。

　ランダム化するなら、こうした「手心」を抜きにして、テキトーどころか厳密にランダムさを追求しなければならない。だが、幸いなことに今ならエクセルを立ちあげて「=rand()」とタイプするだけで、簡単にランダムな数値を得ることもできるのだ。

　こうしたランダム化の力を「デタラメに決めるなんて無責任な」、と感じるおっさんたちもあなたの職場にはいるかもしれない。だが、今ではアメリカの政府ですらこうしたランダム化の力を認め取り入れている。

　政策を実施する前にランダム化を行なうよう求める州法はすでに数千という数にも及び、公立学校の進学から裁判官の管轄まで多くの行政プロセスにランダムさが行きわたり、常にさまざまな実証評価が行なわれている。何せオバマ大統領が二度の大統領選で勝利した一因にも、資金集めや投票の呼びかけにおいてダン・シロカーが導入した膨大な数のA／Bテストを行なったことが挙げられるぐらいである。

　日本には「バカの考え休むに似たり」という素晴らしいことわざがある。そして我々人間は基本的にバカなのだと私は思っている。いくら考えてもわかるわけがないことに対して、よく考えたり話しあえばわかるようになるだなんて思うこと自体、たいへんバカな思いあがりなのではないだろうか。

　私たちにできることは、まずランダムさによって運を天に任すことであり、そして統計解析によってその天の思し召しに耳を傾けることだけなのである。