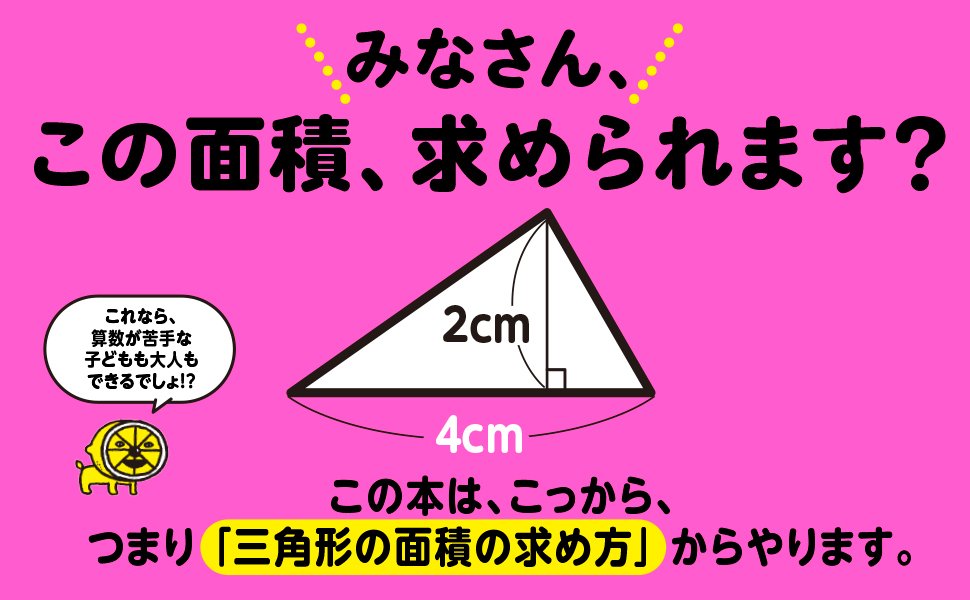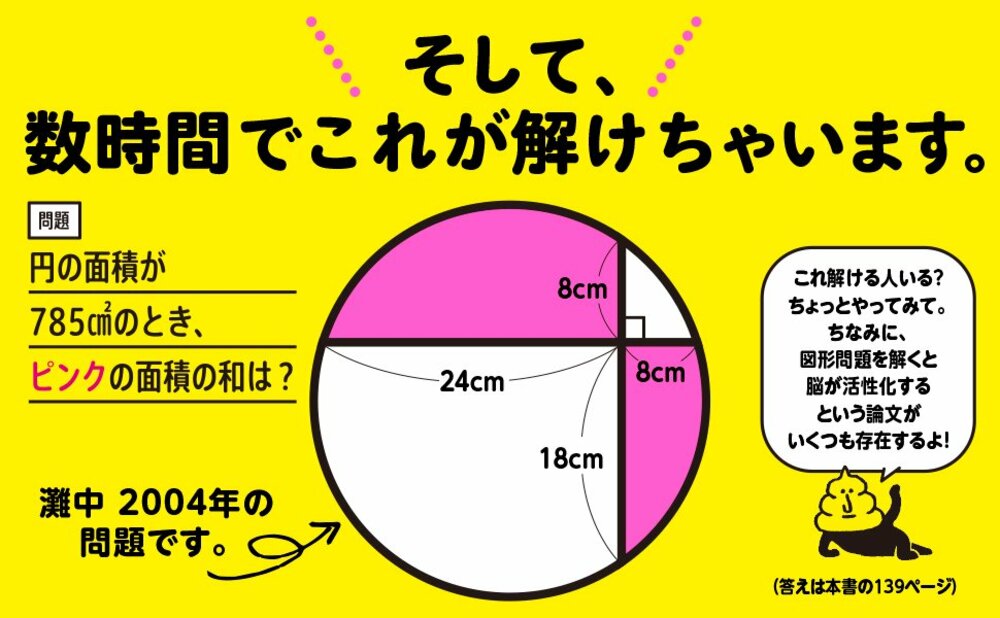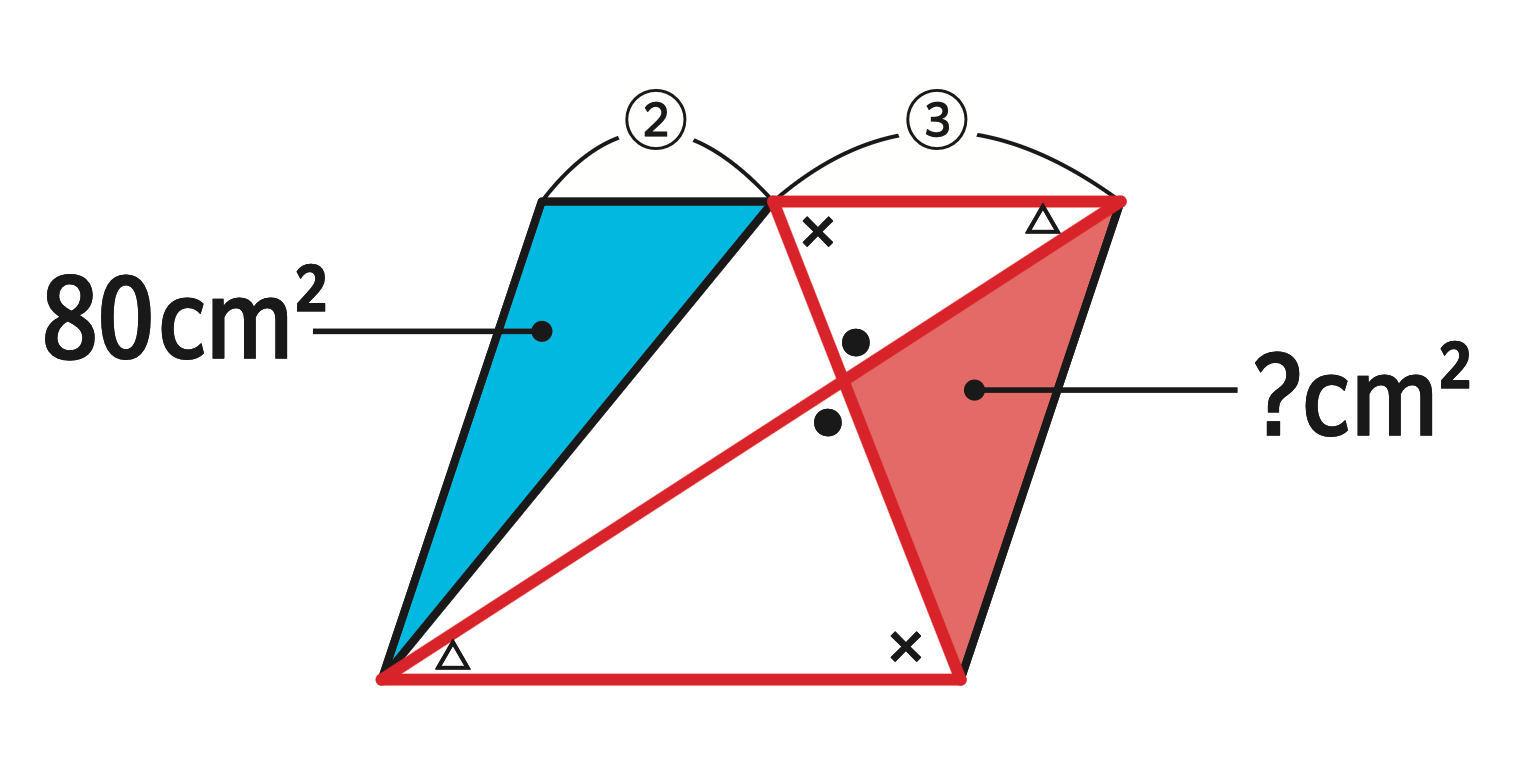
このふたつの三角形は全ての角が同じ大きさになるので、「同じ形の図形」ということになります。
これがふたつ目の武器。
『たった1日で誰でも開成・灘中の算数入試問題が解けちゃう本』（ダイヤモンド社刊より）
ここで、三角形EDFと三角形CBFの辺の比を考えます。
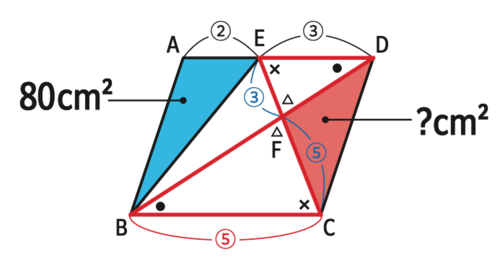
AE:ED＝2：3なので、平行四辺形の向かい合う辺であるBCは2＋3で5になります。
つまり、ED:BC＝3：5。
先ほど説明した通り、同じ形の図形において、対応する辺の比は全て同じになるので、
EF：FCも3：5になります。
ここで、三角形EDCだけを取り出してみましょう。
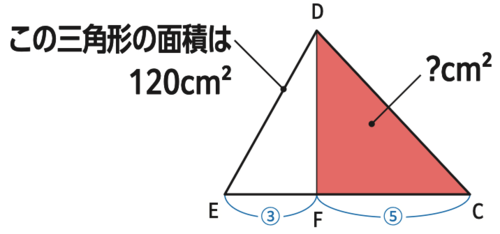
さっき計算した通り、この三角形の面積は120㎠です。
そして、三角形EDFと三角形DFCは高さは同じ三角形になるので、また先ほどの武器が使えます。
『たった1日で誰でも開成・灘中の算数入試問題が解けちゃう本』（ダイヤモンド社刊より）
つまり、EF：FCが3：5なので、三角形EDFと三角形DFCの面積比も3：5になります。
全体の面積は120㎠なので、求めたい三角形DFCの面積は、
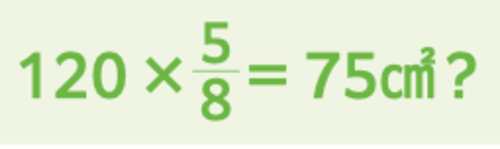
になります。
というわけで、答えは、75㎠でした！
みなさん、解けましたか？
本書の内容
マンガ「20年前の忘れられない光景」
1時間目
「てっとり早く、頭をよくする方法」と
「友だちを簡単に作る方法」
1時間目-1 てっとり早く、頭をよくする方法
1時間目-2 友だちを簡単に作る方法
2時間目
幸せになるコツと比の話
2時間目-1 幸せになるコツと比の話
3時間目
もう灘中が解けちゃう！
3時間目-1 もう灘中が解けちゃう！
3時間目-2 ○＋×＋90°＝180°
4時間目
パズルみたいな算数問題
4時間目-1 パズルみたいな算数問題
5時間目
いよいよ開成中に挑戦！
5時間目-1 いよいよ開成中に挑戦！
5時間目-2 君たちは天才的な補助線が引けるか？
5時間目-3 ほんとうに灘中が解けちゃうの？
【巻末 袋とじ】
これ解けたら、マジで天才！ いや、神です。
正答率、なんと0％。
『たった1日で誰でも開成・灘中の算数入試問題が解けちゃう本』 菅藤佑太 著
