「まじめに勉強に取り組むだけではなく、テクニックを使って1点でも点数を取る。それも実力」。
偏差値35から東大合格を果たした『5科目50年分10000問を分析した東大生のテストテクニック大全』(ダイヤモンド社)の著者・西岡壱誠氏はそう語ります。では、その1点はどう取るのでしょうか。本記事では、本書よりテストで使えるテクニックを紹介します。
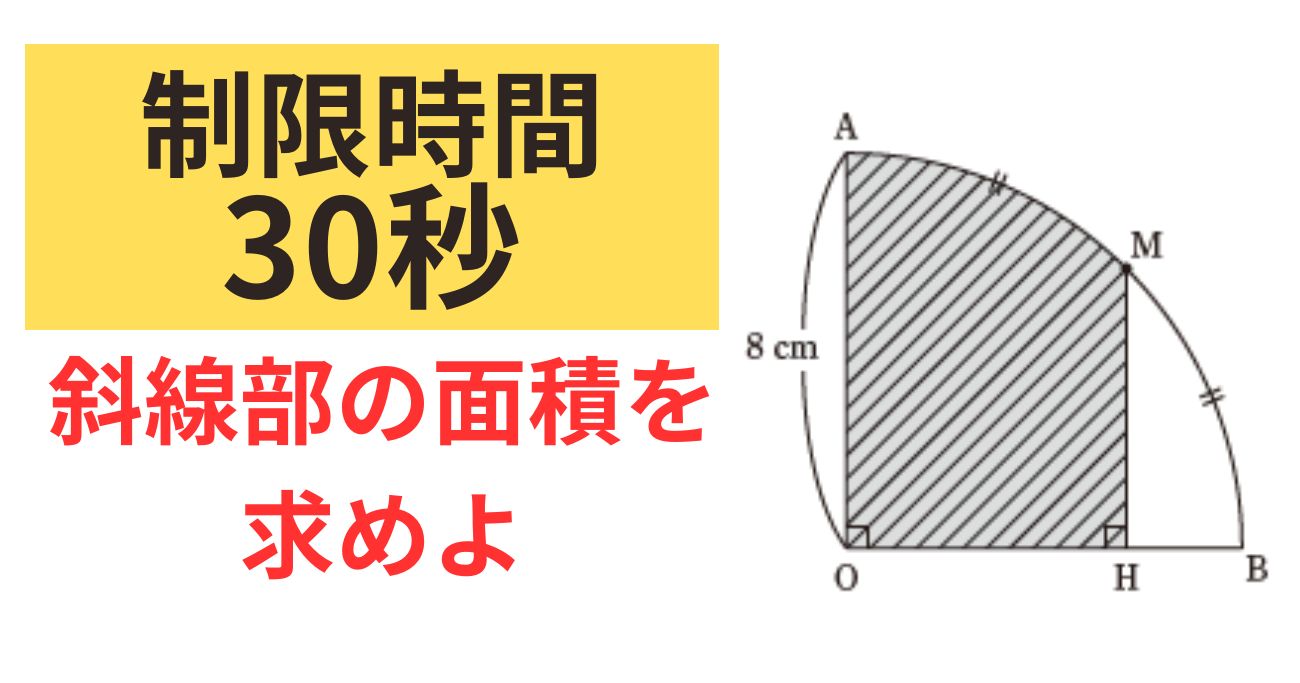
「補助線」はパターンが決まっている
図形問題を解いていると、与えられた図のままでは答えを求めることができず、自分で新しく線を引かないと解けない問題にぶつかることがあります。
この、自分で書き込む線を「補助線」といいます。よく引く補助線というのは、実はパターンが決まっています。
・対角線
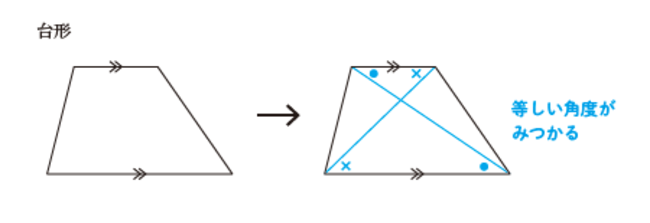
対角線を引くことで要素が増え、考えやすくなることがあります。たとえばひし形は、対角線を引くことで合同な直角三角形を4つ作ることができます。
台形の場合、対角線を引くことで、上底と下底が平行であることを利用して、等しい角度の三角形を作ることができます。知っている形を作り出して「こことここが等しいんだな」という情報を増やしていくことも、補助線を引く意義のひとつです。
・延長線
与えられた図形の中で線が不自然な位置で終わっているとき、さらに延長してみると新しい図形が見えてくる場合があります。特に線分比や相似比を求める問題でよく登場します。
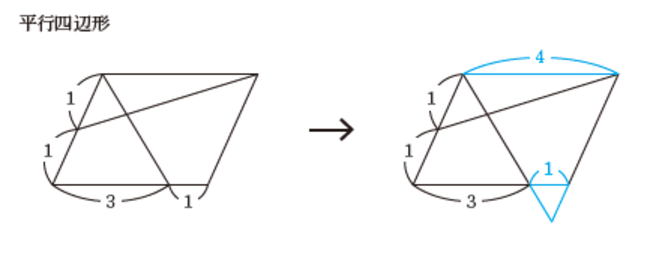
台形や平行四辺形などの有名四角形でない四角形は扱いが難しいので、下の図のように延長線を引くことによって、三角形にしてしまったほうが問題が解きやすくなる場合も多いです。
・平行線
平行線の性質(対頂角・同位角・錯角)、等積変形、平行線と線分比の性質など、「平行線」は情報の塊です。そこで、与えられた図には引かれていない「ある辺に対して平行な線」を補助線として引いてみると、意外と問題
を解くためのヒントが見つかることもあります。

・円の中心と円周上の1点を結ぶ補助線
頻出なのに見つけにくいのが、この「円の中心と円周上の1点を結ぶ補助線」です。この線は、円の中心と円周上の1点を結んでいるので、つまり「半径」ということになります。
円が登場する図形問題において半径の長さは非常に重要な情報となりますし、新たな中心角の情報が増えたり、半径が接線に対し垂直であることが利用できたりして、角度の情報を増やすことにも繋がります。



