【制限時間30秒】斜線部の面積をパッと計算できる？

次の図形問題を解いてみましょう

たとえば次の図形問題。点Oを中心とする中心角90°のおうぎ形で、半径は8cmです。弧ABを2等分する点をMとして、MからOBに垂線を下ろしました。斜線部の面積を求めてください、という問題です。（図1）

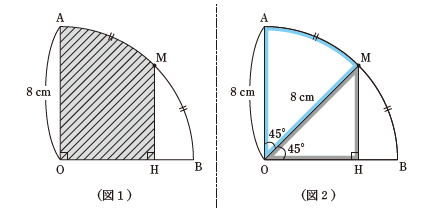
斜線部は、四角形かと思いきや上の辺が曲線なので、そのままでは面積を求めることができません。そこで、円の中心Oと、円周上の点Mとを直線で結んでみます。

OMはおうぎ形の半径なので、長さは8cmです。MはABを2等分するので、OMも中心角を2等分し、∠AOM＝∠BOM＝45°となります。（図2）

すると、斜線部は「半径8cm、中心角45°のおうぎ形」と「斜辺の長さが8cmの直角二等辺三角形」に分けられることがわかります。それぞれの面積を求めると、おうぎ形の面積を求める公式は「（半径）×（半径）×（円周率）×（中心角）/360°」なので、8（cm）×8（cm）×3.14×45（°）/360（°）=25.12（平方センチメートル）

直角二等辺三角形の面積は「（斜辺）×（斜辺）÷4」で求められるので、

8（cm）×8（cm）÷4=16（平方センチメートル）

したがって、求める斜線部の面積は

25.12（平方センチメートル）+16（平方センチメートル）=41.12（平方センチメートル）

答えは、41.12（平方センチメートル）となりますね。

特に4つめの「円の中心と円周上の1点を結ぶ補助線」についてはあまりにも頻出ですので、円やおうぎ形が登場する図形問題においては「中心と結ばれていない円周上の点を見つけたら、まず中心と結んでから考える」と意識するとよいでしょう。

難しい図形問題に取り組むうえで、補助線を引くことはたしかに有効ですが、不必要なところに補助線を引いてしまうと無駄に問題を複雑にしただけで答えに近づくこともできず、かえって混乱を招いてしまいます。

補助線は、「ここかな？」と思ったところに引いて、解きながら「なんか違うな？」と思ったらためらいなく消す、トライ＆エラーの精神が大切です。

なるべく少ない試行回数で正解へと辿り着くために、よく引く補助線のパターンを知っておきましょう。