子どもから大人まで数学を苦手とする人は非常に多いのではないでしょうか。ましてや高校数学ともなるとほとんどの人が挫折してしまった経験を持っているでしょう。しかし、高校数学の基礎は丁寧に学べば特別難しいものではなく、同時に得た知識は私たちの生活にも大きく役立ちます。そんな高校数学の超入門書として書かれたのが『【フルカラー図解】高校数学の基礎が150分でわかる本』です。本記事でははじめての人から大人の学び直しまで1人で高校数学が学べる本として発刊された本書より内容の一部を抜粋してお届けします。
 Photo: Adobe Stock
Photo: Adobe Stock
期待値とは
期待値は、平均してどれくらいのスコアが見込めるかを表す数値です。例として、確率30%で2000円もらえ、確率70%で1000円もらえる宝くじを買ったとします。このとき、平均して何円くらいもらえると考えるのが自然でしょうか。
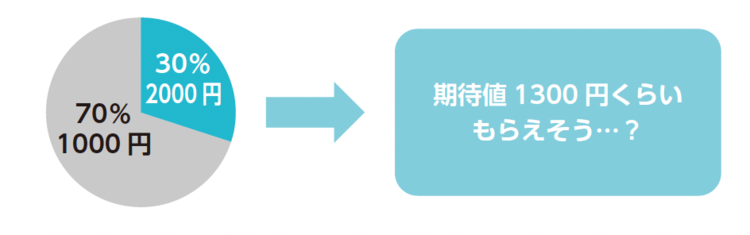
1000円では少なすぎますし、1500円では逆に多すぎますが、1300円程度と考えると自然でしょう。これが期待値の考え方です。
期待値を計算する方法
期待値は、「スコア×確率」の合計で計算することができます。たとえば、先程の宝くじの例の場合、「スコア×確率」はそれぞれ
・当たった場合:2000円×0.3=600円
・ハズれた場合:1000円×0.7=700円
となるため、期待値は600+700=1300円となります。
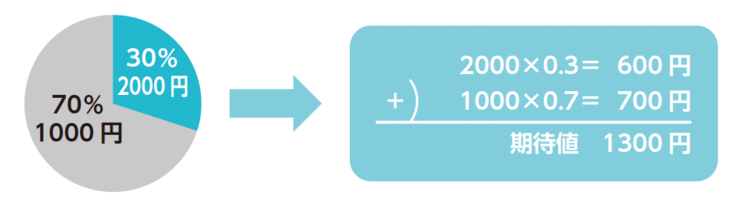
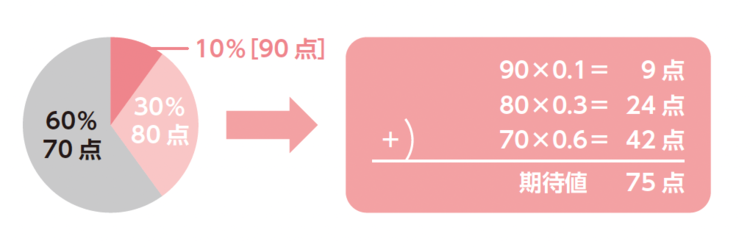
また、数学の期末テストの結果が10%の確率で90点、30%の確率で80点、60%の確率で70点になるとします。このとき「スコア×確率」は
・90点の場合:90点×0.1=9点
・80点の場合:80点×0.3=24点
・70点の場合:70点×0.6=42点
となるため、得点の期待値は9+24+42=75点です。
練習問題
太郎君は、確率2%で1等の1万円、確率8%で2等の3000円、確率90%で3等の0円となる宝くじを買いました。得られる金額の期待値は何円ですか。カッコの数字を埋めてみましょう。
(スコア)×(確率)は、
1等のとき( )×( )=( )円
2等のとき( )×( )=( )円
3等のとき( )×( )=( )円
期待値は、これをすべて足した( )円



