マッキンゼーの元パートナーが回帰分析で肥満を分析してみた

知る人ぞ知る問題解決メソッド、「問題解決の7ステップ」がついに書籍化する――。マッキンゼーで最も読まれた伝説の社内文書「完全無欠の問題解決への7つの簡単なステップ」の考案者であるチャールズ・コン氏みずから解説する話題書『完全無欠の問題解決』（チャールズ・コン、ロバート・マクリーン著、吉良直人訳）が注目を集めている。マッキンゼー名誉会長のドミニク・バートンは「誰もが知るべき、誰でも実践できる正しい問題解決ガイドがようやく完成した」と絶賛、グーグル元CEOのエリック・シュミットも「大小さまざまな問題を解決するための再現可能なアプローチ」と激賞している。本書では、「自宅の屋根にソーラーパネルを設置すべきか」「老後のためにどれだけ貯金すればいいか」といった個人の問題や「販売価格を上げるべきか」「ITの巨人に訴訟を挑んでいいか」といったビジネス上の問題から、「HIV感染者を減らすには」「肥満の流行をどう解決するか」といった極めて複雑なものまで、あらゆる問題に応用可能なアプローチを紹介している。本稿では、本書より内容の一部を特別に公開する。

Photo: Adobe Stock

肥満と相関する変数を見つける

　肥満の蔓延と増加には複数の説明が存在し、地域社会によって大きく異なり、複雑な行動や政策の要因が作用している。さらに、私たちが知るかぎり、どのような規模の地域社会においても、この傾向を逆転させたというサクセスストーリーは存在しない。

　この例では、回帰分析は肥満問題の根本的な要因を理解するための強力な分析ツールであることを強調したいと思う。回帰分析が肥満という難問を解決するわけではないが、解決策を示す場所を教えてくれる。

　私たちは、研究助手の1人で、ゲノム研究とビッグデータ分析の博士号を取得しているローズ奨学金受賞学者のボグダン・クネゼヴィチに、回帰分析を使って都市レベルでの肥満に関するいくつかの仮説を検証するよう依頼した。この仮説はマッキンゼー・グローバル・インスティテュート（MGI）が行った肥満に関する包括的な調査から導かれたものである[＊1]。

　ボグダンは、アメリカの68都市について、肥満者比率[＊2]、教育水準、世帯収入の中央値、都市の歩きやすさ[＊3]、気候の快適性スコア[＊4]などのデータを収集した。気候の快適性スコアは身体活動への天候の適合性を示すもので、気温と相対湿度の合計を4で割って計算される。快適性スコアは「ゴルディロックスのお粥」のようなもの、つまり熱すぎず冷たすぎず、温度と湿度がちょうど良い状態を表している。

　ボグダンの回帰分析の結果、教育、収入、街の歩きやすさ、快適性スコアのすべてが肥満と負の相関にあることを示した。また、歩きやすさを除くすべての変数が、個別に肥満と相関していることを発見した。

　おそらく驚くべきことに、快適性スコアと歩きやすさの間にはほとんど相関がなかった。他の変数、特に収入と教育の間には高い相関があり（68％）、因果関係における相対的な影響度合を判定することが難しくなる可能性を示していた[＊5]。

　図表1では、各都市のボディ・マス指数（BMI）で測定した肥満者比率と世帯収入を比較したもので、快適性スコアは円のサイズとして示されている。肥満と収入の間の相関関係は大きく明確であり、都市間の肥満の分散の71％は収入で説明できる。

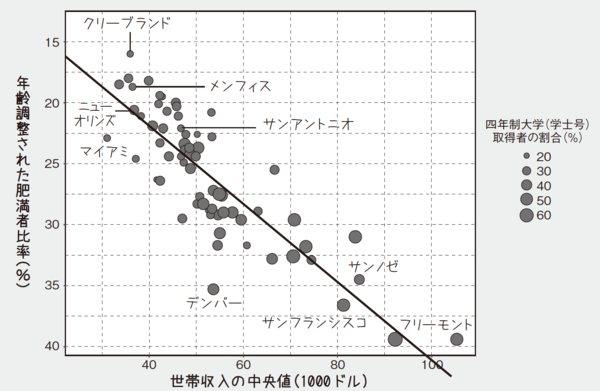図表1　収入、学歴および肥満の関係

　各点から導かれた近似直線からは以下のことが見て取れる。つまり、世帯収入が8万ドルの家計と6万ドルの家計を比べると、前者は後者よりも肥満人口比率が7％ポイント低いのである。

肥満を82％説明する4つの変数とは

　都市間の肥満度の違いを把握するのに最適なこのモデルは、世帯収入、教育水準、快適性スコア、街の歩きやすさ、そして収入と教育水準の2変数間の関係を説明する相互作用項の組み合わせによって決まる。すべての変数は統計的に有意であり、肥満と負の相関があった。4つの変数すべてを含めると、肥満の分散の約82％が説明できる。

　これは、私たちの経験上比較的高い説明力の水準である。ロバート・ウッド・ジョンソン財団などの非営利団体は、アメリカにおける肥満の差を説明するうえで、収入と教育水準の要因がいかに重要であるかを指摘している。

　複数の説明変数を用いる重回帰分析では、変数を組み合わせてコントロールすることで、根底にある変数間の関係を説明することができる。たとえば、歩きやすさだけを使って線形回帰分析を実行すると、都市の歩きやすさと肥満率の間には有意な相関がないと結論づけられる。しかし、重回帰分析で歩きやすさと快適性スコアの両方を組み合わせると、天候をコントロールしたうえで歩きやすさと肥満の間に有意な相関があることがわかる。

　この例は、回帰分析が問題の要因を理解するのにどのように役立つのかを示している簡単な例である。おそらく、都市レベルで積極的な政策介入をするための戦略を開発するのにも有用だろう。

　回帰分析は、理解を深めるのに役立つが、考慮すべきいくつかの落とし穴もある。

回帰分析の落とし穴
・相関関係と因果関係は別であることには注意が必要である。歩きやすい都市は、ほとんどの場合、歩きにくい都市よりも肥満率がはるかに低いようである。しかし、統計からだけでは、都市の歩きやすさが肥満率を下げる真の要因であるかどうかを知る方法はない。おそらく、歩きやすい都市は物価が高いので、本当の要因は社会経済的地位の高さなのかもしれない。あるいは、健康な人は、歩きやすい地域に転居しているのかもしれない
・モデルでは考慮されていないが非常に重要な変数があるかもしれない場合、回帰モデルは誤解を招く可能性がある。このモデルは都市レベルで構成されているため、個人レベルの行動や文化的要因のことは認識しておらず、モデルに反映されていない
・説明変数を追加すると回帰分析のパフォーマンスが向上するかもしれないが、変数を追加するとデータの過剰適合になる可能性がある。これは、回帰分析の基礎になる数学の問題である。現象を十分に説明できるモデルの中で、常に最も単純なものを使用すべきであることを忘れないでほしい

（本原稿は、チャールズ・コン、ロバート・マクリーン著『完全無欠の問題解決』を編集・抜粋したものです。この伝説の問題解決メソッドについてはこちらの記事で詳しく説明しています）

【著者プロフィール】
チャールズ・コン
ハーバード大学、ボストン大学卒業、およびローズ奨学生としてオックスフォード大学大学院修了。ボストン コンサルティング グループでキャリアを開始した後、マッキンゼー・アンド・カンパニーのパートナー、ティケットマスター・シティーサーチ社の創設代表取締役、オックスフォード大学ローズ奨学金財団CEOを歴任。100年を超える歴史を持つ財団組織において、学者のための問題解決トレーニング・プログラムの開発を含む戦略と運営を刷新するための改革を成功させる。ほかにもパタゴニア、南アフリカのマンデラ・ローズ財団、アルカディア財団など、数多くの企業や財団の理事会、役員会に参加。ゴードン＆ベティ・ムーア財団の上級顧問を務める。野生のサーモンの生態系イニシアティブとパルミラ環礁研究ステーションを含む環境保護プロジェクトに参加。

ロバート・マクリーン
ニューイングランド大学（オーストラリア）卒業、コロンビア大学ビジネススクール修了。マッキンゼー・アンド・カンパニーの名誉ディレクター。オーストラリアとニュージーランド共同事務所の総責任者として8年間同社を主導し、グローバル・ディレクター委員会委員を務める。オーストラリア経営大学院学部長、オーストラリア最大の慈善財団であるポール・ラムジー財団理事を歴任。オーストラリアとアジア地域の自然保護区の管財人として、湿地での水質保全、貝類の種の回復、都市の緑地からもたらされる人間の健康の改善に取り組んでいる。ビジネス、社会福祉、環境への貢献により、2010年オーストラリア勲章を受章。

吉良直人（きら・なおと、翻訳）
国際基督教大学教養学部卒業。ハーバード大学経営大学院修了（MBA）。帝人未来事業部、帝人ボルボを経て、マッキンゼー・アンド・カンパニージャパンに入社。以来、大前研一氏の同社退職まで共に働いた。『マッキンゼーが予測する未来』（ダイヤモンド社）ほか訳書多数。

---

マッキンゼー名誉会長　ドミニク・バートンからのメッセージ

「完全無欠（ブレットプルーフ）」。マッキンゼーでは、問題解決者としての評判にどこから攻撃を受けても守れる防弾処理を行ったという意味で「完全無欠の」という表現を超える褒め言葉はない。現代のコンサルティング会社を機能させるには、多くのスキルと多様な種類の知性が必要だが、基礎となる能力は常に創造的な問題解決力である。

　近年、経済的および技術変化のペースが加速するにつれ、優れた問題解決の重要性は増大し、それに伴って対処しなければならない問題の範囲や複雑さも増している。

　今日私たちは、消費者向け新製品のデジタルマーケティング戦略を開発するために雇われるのと同じように、ある国の公衆衛生システムが次のエボラ出血熱発生に備える支援のために雇われる可能性がある。より多くのデータが利用可能になるにつれて、思考の質の基準も高まっている。だからこそ、完全無欠の問題解決者が必要とされている。

　産業界であれ、非営利団体であれ、政府機関であれ、新しい組織構造や運用ルールがこれからどうなるかを予測し、計画することは不可能である。また、従来のドメイン指向のトレーニングアプローチを単に推進し、適応させるだけでは十分ではない。このレベルの変化をうまく乗り越える唯一の方法は、流動的で創造的な問題解決者になることである。

　世界経済フォーラムが21世紀に最も求められるスキルに「複雑な問題解決スキル」を挙げたのは、このためである。あらゆる組織が、人材採用にこの能力を何よりも求めている。

　学校や大学で規律ある包括的な問題解決アプローチが教えられていないことは、驚くべきことだろう。多くのビジネススクールでさえ、ほとんどのカリキュラムに存在しない。根本原因分析や、現在流行しているアジャイルチームやデザイン思考などの要素を見ることはできるが、十分ではない。本書は、私たちがマッキンゼーで長年実践してきた実績のある方法論をアレンジし、これまでなかった問題解決の体系的なプロセスを紹介するものである。

あらゆる問題に使える完全無欠の問題解決メソッド

　本書の著者であるチャールズとロブが示している7ステップの方法は、明白でわかりやすいものだ。専門的なスキルや派手な数学の才能は必要ない。本書は、この洗練された分析技術がどのような場合に価値を発揮するのか、そしてなぜそうした技術が一般に思われているよりも身近なのかを示している。

　この方法は反復的で柔軟性があり、素早く適用して大まかな回答を得たり、じっくり適用して微妙なニュアンスを含むよう微調整した回答を得たりすることができる。

　また本書は、近年明らかになった意思決定における人間のバイアスに抗う方法を示している。個人的な人生の決断から、ビジネスや非営利団体の問題、社会が直面している最大の政策課題まで、ほぼすべての種類の問題に有効である。

　長年ランナーである私は、膝の手術を受けるかどうかについてのロブの分析に特に惹かれた。また、漁業や教育資金などに関する複雑な政策決定に対して、有権者が対応を検討するのに役立つわかりやすい分析にも感銘を受けた。

　当然、事業戦略や収益性向上などの分析も楽しく読んだ。社会・環境問題には本当に手に負えないものがあるが、この方法論は、気候変動や肥満対策など、最も厄介な問題の解決にも光を当てることができる。

　この種の本を書くのに、この2人の著者以上にふさわしい人はいないだろう。チャールズは、私たちがトロント事務所の若手コンサルタントだったときに、マッキンゼーの問題解決に関する社内資料として「完全無欠の問題解決への7つの簡単なステップ」を起草した。この資料は、世界中のマッキンゼー事務所から最も閲覧要求の多かった専門能力開発文書の1つとなった。

　また、私はロブとは35年以上の付き合いで、初めて彼に会ったのは、オーストラリア最大企業のCEOの時間をいかに活用するかというプロジェクトを一緒に取り組んだのが始まりだった。

　チャールズとロブはマッキンゼーにいる間、他の同僚と協力し合い、現在も使われている「成長戦略のための地平線までのアプローチ」を開発した。彼らが会社を辞めた後でも、起業家として、そして非営利セクターの変革者として、問題解決メソッドを実践し続けているのを見るのは楽しかった。近年では、チャールズがローズ財団の戦略開発と変革にこの独特の考え方を導入するのを、私は間近で見た。

　問題解決力は21世紀のコアスキルである。誰もが知るべき、誰もが実施できる正しい問題解決ガイドがようやく完成した。

マッキンゼー・アンド・カンパニー　元マネージング・ディレクター
ドミニク・バートン
（『完全無欠の問題解決』序文より）

---

【ダイヤモンド社書籍編集部からのお知らせ】
『完全無欠の問題解決』

『完全無欠の問題解決』
チャールズ・コン、ロバート・マクリーン著、吉良直人訳　定価：2970円
発行年月：2022年9月

　マッキンゼー名誉会長絶賛、グーグル元CEO激賞！ マッキンゼーで長らく実践されてきた伝説の社内資料「完全無欠の問題解決のための7つの簡単なステップ」がついに書籍化。不確実性が高い問題や利害関係者が多すぎて解決困難な「厄介な問題」にも完全対応。大学生から経営者まで誰もが学ぶべきビジネススキルがここに！