統計学の解説書ながら42万部超えの異例のロングセラーとなっている『統計学が最強の学問である』。そのメッセージと知見の重要性は、統計学に支えられるAIが広く使われるようになった今、さらに増しています。そしてこのたび、ついに同書をベースにした『マンガ 統計学が最強の学問である』が発売されました。本連載は、その刊行を記念して『統計学が最強の学問である』の本文を公開するものです。第31回では、「ベイズ統計」について解説します。（本記事は2013年に発行された『統計学が最強の学問である』を一部改変し公開しています。）
Photo: Adobe Stock
ベイズ派と頻度論派の確率をめぐる対立
ここまでに社会調査や心理統計学、データマイニングや計量経済学といったさまざまな分野における統計学に対する考え方の違いを紹介したが、最後に分野をまたいで存在する「確率自体の考え方」についての対立を紹介しよう。
それが頻度論者かベイズ論者か、という対立軸である。両者の違いを一言で表すとするならば、「事前に何らかの確率を想定するか」「しないか」と言い換えてもいいかもしれない。
両者の違いを理解するために、たとえばここに2種類のコインがあったとしよう。一方は表が出る確率も裏が出る確率も5分5分の「本物のコイン」で、もう一方は表が出る確率が8割、裏が出る確率が2割の「イカサマのコイン」だ。両者は見た目や重さなどからはまったく区別がつかないものとするが、何回か投げた回数を集計・分析し、どちらのコインであるかをそれぞれの立場から判断してみよう。
頻度論派はシンプルに考える
頻度論すなわちフィッシャーのような考え方に基づく統計家が、たとえば10回投げたうち10回とも表が出た、というデータを得たとする。このコインは本物のコインだと言えるだろうか？
彼はおそらく、まずこのコインが本物だと仮定する。そしてその仮定のもとで10回中全部が表になる確率を計算するだろう。すなわち、「2分の1の確率で出る表が偶然10回全部出る確率は2の10乗分の1、つまり約0.10％しかない」ということだ。第14回で紹介したミルクティにうるさい夫人が「もしデタラメに答えていたとして10杯全部を当てる確率」とまったく同じ計算であり、この0.10％という確率はいわゆるp値と呼ぶものである。つまり、このような確率の奇跡が起こったと考えるよりは、そもそもの「このコインは本物」という仮定を「考えにくい」と捨て去ったほうが理にかなっているという判断を行なうのだ。
次に「このコインはイカサマのコイン」だと仮定したらどうなるだろう？ 先ほどと同様の計算を行なえば、「80％の確率で出る表が偶然10回全部出る確率は10.74％程度」ということになる。p値が10.74％程度なら別に奇跡的と言うほどではない。だからこの仮定を捨てきることはできない。
一方の「本物のコイン」という仮説が捨て去られ、他方の「イカサマのコイン」という仮説は捨て去ることができないのであれば、すなわちこれはイカサマのコインだと考えたほうが妥当だということになる。もっと簡単に考えたければ、とりあえず1万回ほどコインを投げてみて、そのうち何回が表になるかをカウントしてみればいい。おそらく本物のコインなら5000回前後しか表が出ないし、イカサマのコインだったら8000回前後表が出る。頻度論とは確率をこうした「何回中の何回」といった「頻度」でとらえようという意味である。なお、このとき本物のコインで8000回前後の表が出るp値も、イカサマのコインで5000回前後しか表が出ないp値も著しく低い。
ベイズ派は「事前確率」と「事後確率」を考える
一方、ベイズ論者がこのコインを見分けようとすると、まず何の情報もない時点で、どの程度の確率でこのコインは本物かイカサマか、と考える。なおこの確率のことを事前確率と呼ぶ。事前確率は別にどのような値に設定してもかまわない。コインを持っている相手の人相が悪いから、7：3でイカサマの可能性が高いと考えることもベイズ的には何の問題もないのだが、ここではひとまず半々だったと想定し、先ほどと同じく「10回投げたうち10回とも表が出た」という結果から推測を行なおう。
コインが本物だった場合に10回全部が表になる条件付き確率も、イカサマのコインだった場合に10回全部表になる条件付き確率も、頻度論と計算方法は変わらずそれぞれおよそ0.10％あるいは10.74％であるが、その次の計算方法がベイズでは少し異なる。
すなわち、本物だった場合、イカサマだった場合のそれぞれの状況において、事前確率と条件付き確率の掛け算を行なうのだ。この場合、以下のような計算が行なわれる。
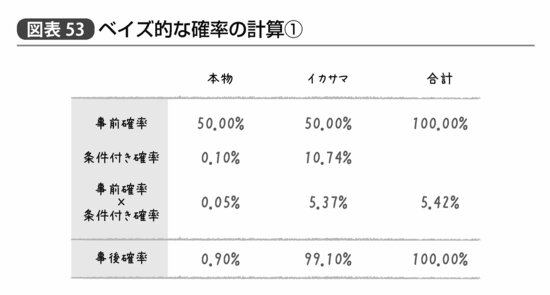
①本物である事前確率×本物である場合に10回全部が表になる条件付き確率
≒ 50％×0.10％
≒ 0.05％
②イカサマである事前確率×イカサマである場合に10回全部が表になる条件付き確率
≒ 50％×10.74％
≒ 5.37％
また、コインが本物かイカサマかという選択肢しかない以上、どんなときでもコインが本物である確率とイカサマである確率を合計すれば必ず1になるはずである。それは「10回全部が表になった」という結果が得られた時点においても例外ではない。つまり、①と②の合計値は「1」になるはずなのだ。
もう少し詳しく説明すると、①「本物のコインが投げられて10回連続表である」0.05％の確率と、②「イカサマのコインが投げられて10回連続表である」5.37％の確率の合計は5.42％になる。これはコインを投げる前に「コインが本物かイカサマかが5分5分の状況で10回連続表になる確率は？」と聞かれたときの答えである。
だが、「コインが10回連続表になった状態で、コインが10回連続表になる確率は？」と聞かれれば、当たり前のように100％である。「人間が人間である確率は？」と聞かれているのとまったく同じ質問だ。哲学的な深みにはまらず素直に答えれば、誰でも100％だと答えられるはずである。
だから「コインが10回連続表になった状態でコインが本物である確率は？」と聞かれれば、この100％となるはずの5.42％という確率に占める0.05％という確率の割合を考えればいいし、「コインが10回連続表になった状態でコインがイカサマである確率は？」と聞かれれば、同様に5.42％という確率に占める5.37％という確率の割合を考えればいい。
そこで、①と②の合計値である5.42％という値で、①、②それぞれの値を割ってやる。そうすると「10回全部が表になる場合にこのコインが本物である確率」は、
①÷（①＋②）≒0.05÷5.42≒0.90％
であり、一方「10回全部が表になる場合にこのコインがイカサマである確率」は、
②÷（①＋②）≒5.37÷5.42≒99.10％
と計算することができる。
すなわち、10回全部が表になったデータから、これは99.1％の確率でイカサマのコインであるとベイズ論者は判断するのである。このように事前確率とデータに基づいて算出された確率のことを事後確率と呼ぶ。
このような計算結果をまとめると図表53のようになる。
ちなみにベイズというのはこうした確率の考え方を短いエッセイの中に示した牧師の名前であり、彼の死後に数学者であるラプラスによって彼の考え方は広められた。
計量経済学と相性がいいベイズ統計
これまでに紹介した分野別の傾向で言えば、社会調査、疫学、生物統計学、心理統計学分野には頻度論者が多く、計量経済学者にはベイズ論者が増えており、データマイニング屋は特にどちらとも意識していないがベイズ論者寄り、といったところだろうか。
同じ統計家の中でも頻度論者とベイズ論者の対立は根深く、頻度論者からすれば「事前確率を設定する」という考え方が気持ち悪くて仕方がない。異なる事前確率を想定していれば、99.1％イカサマという事後確率が異なるものになっていたのである。そんなどうとでもできる確率が得られたところで、いったい何の意味があるというのかというのが彼らの主張だ。
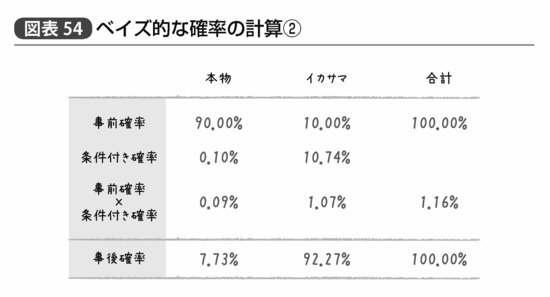
ベイズ論者からすれば、もし仮に最初の事前確率として90％これは本物であると考えていても、「10回全部表」というデータから導かれる事後確率は「92.27％イカサマ」であり、事前確率による影響は小さいと主張したいだろう（図表54）。
一方で、たとえば3回しかコインを投げられなかった状態で頻度論は「どちらかはわからない」としか判断できないが、ベイズ的な考え方であれば、少なくともどちらである可能性が高いかは判断できるのだ。
そのため「間違いが許されない」という保守的な判断が求められる分野ほど頻度論に基づく傾向にある。たとえば医療の中でも「新しい薬の使用を承認すべきか」という判断は最も間違いが許されないものの1つである。何の効果もない薬に医療保険という「みんなのお金」が使われるということは倫理的に許されることではないし、それによって誰かの命が失われるかもしれないのだ。
そのため回帰モデルによる調整や、傾向スコアの使用すら許されず、ランダム化比較実験を行なった結果、誤差とは考えられないレベルの有効性を示したものだけが承認される、というのが国際的な常識である。こうした間違いの許されない判断においては「仮に効くか効かないか五分五分だと仮定して～」という事前確率などもってのほかである。因果推論をミスリードし得る仮定なんて極力ないほうがいい。
国の公的なデータを作ることに長年苦心してきた社会調査の統計家にしても、「もし仮に失業率が3％だとして～」などという仮定は誤りのもとになりうるし、もともと大量のランダムサンプルでよい推定値を得ることが前提の社会調査分野において、ベイズ的に考えるメリットは小さい。過疎地域やマイノリティを対象にした調査で、一部ベイズ的な手法が用いられることがあるくらいだ。
一方で、頻度論とベイズのどちらが演繹的推論と相性がいいか、と考えれば近年計量経済学者にベイズ論者が増えていることにも頷けるだろう。ベイズ的な考え方であれば、「事前確率」という仮定を置くとデータからどういったことが言えるか、という演繹が可能になる。
経済学は100年以上の演繹の歴史の中で生みだされた多数の理論的なモデルを持っている。経済学者にとっては今この場で得られた現実のデータ自体も重要だが、それ以上に100年以上の歴史で培われた理論を信頼してもいるだろう。だとすれば、単純に「理論なき計測」で得られたデータにただ回帰モデルを当てはめるよりも、「理論に基づけば回帰係数がどのような確率でどのような範囲の値をとるか」、という事前確率を仮定できるベイズ的な推定方法のほうが理論を有効に活用することができる。
さらに言えば、経済学の理論はもともと曲線的なモデルを考えていたり、「理論上グラフはここまでの値しか取り得ない」といった演繹の結論を得ていたりもする。こうしたモデルを推定するうえで、単純に数理的な性質としてもベイズ的な推定は威力を発揮しやすい。
迷惑メールの判別に威力を発揮するベイズ統計
またデータマイニングにおいてもベイズ的な手法が存在している。最も有名なのは迷惑メールを判別するアルゴリズムだろう。
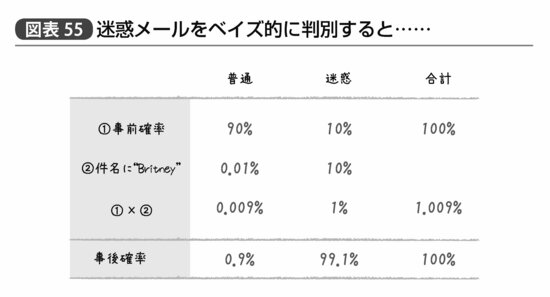
たとえば一般的な日本人に届くメールの1割ほどが迷惑メールだ、ということがこれまでのデータ上明らかになったとする。そして普通のメールと迷惑メールそれぞれの件名を見ていくと、迷惑メールのうち1割には「Britney」つまりブリトニー・スピアーズの無料エロ動画やスキャンダルについての内容だったとわかったとする。もちろん普通の日本人がブリトニー・スピアーズのことについてわざわざ英語でメールすることは全メールの0.01％もない。
この状況で「Britneyという単語が件名に入ったメール」を判別すると、図表55で示すように、先ほどのイカサマのコインと同様の計算から99.1％の事後確率でこのメールは迷惑メールだとわかる。
こうした手法は医薬品の承認とは異なり、「多少間違ってもいいから迅速にある程度の確率で正解が得られればいい」という考え方に基づいて用いられている。
頻度論に基づくと、受け取ったメールを十分に蓄積してから、「Britneyという単語が件名に入っているメールが普通のメールである確率はとても低い」と考えることはできるが、迷惑メールから1秒でも早く解放されたければベイズ的に考えたほうがいい。どうせ使い続けるうちに事後確率は少しずつ修正されて、間違った分類も減っていくのである。
これまでの分野間の考え方と同様、ベイズと頻度論のどちらが正しくてどちらが間違い、というものではない。限られた情報と仮定を組み合わせる「効率のよさ」が求められるならベイズを使えばいいし、「可能な限り間違う可能性を減らしたい」とか「十分なデータを利用できる」のであれば頻度論的にp値を求めたほうがいいだろう。
これだけさまざまな分野で統計学が用いられるようになると、自分と異なる分野の異なる考え方で用いられる統計手法の意味を理解するのも一苦労である。しかしながら、自分の習った統計学と考え方が異なるという理由で拒絶したり、見当違いな批判を行なうことはたいへんもったいない。それよりも、この章で紹介したような統計家たちの考えの違いをきちんと理解し、異なる立場で培われた知恵を自分の必要に応じて活用することのほうがよっぽど賢明なやり方である。
統計学はそれ自体最強の学問だが、その最強さをさらに盤石なものにするためには、ありとあらゆる統計学の考え方に対してオールラウンダーになることが求められるのである。
▶『マンガ 統計学が最強の学問である』の刊行に寄せて
『マンガ統計学が最強の学問である』は、言語化・定型化された仕事がAIに奪われていくなかで、「新たに何をするか考えて決める」スキルを日本に最大限広げるために制作されました。
実は初代『統計学が最強の学問である』はほとんど数式を使わず、統計学がどう生まれてどう役に立てられるのかにフォーカスした、統計学の本としては少し変わった本でした。しかし、40万部以上売れただけあって、あの本を読んで統計学を面白いと感じ、本格的に勉強しようとしたり、実務に活かすようになった、という方と私は日々の仕事の場で頻繁にお会いします。統計手法の数理面を細かく説明したり、統計解析をおこなうためのプログラミングに関する本は多数ありますが、それはちょうどAIのサポートが手厚くなっている部分です。今の時代はそれよりも、「統計学を活用したい」というモチベーション、「どのような課題に対して統計学を活用するか」という課題設定のコツ、そして分析結果の読み解き方と、結果を踏まえて何をやるべきかを考える枠組みといったスキルのほうが相対的に重要になってきているのではないでしょうか。
本書が目指すのは、まさにそうした今こそ必要な「統計学の活かし方」を、物語を通して皆さんにお伝えすることです。たとえば『SLAM DUNK』というマンガを読むことでバスケットボールをプレイするモチベーションが喚起されたり、バスケットボールの観方がわかるようになったりといった方がたくさんいるように、すばらしいマンガは多くの人の人生を変える力を持っています。ありがたいことに私にとっても大好きな漫画家であるうめさん（小沢高広さんと妹尾朝子さん）に漫画制作を依頼できたことで、ストーリー面でも作画面でもすばらしいものになりました。私自身のデータ活用に関わる経験を凝縮した物語を、うまく追体験していただければ幸いです。
また各話の最後には、それまでに出てきた統計手法について、できる限りわかりやすく、かつ簡潔に説明した解説を加えました。ストーリー内ではあまり説明臭くならないよう、しかし気になるであろう知識面はその後の解説で補足できるよう個人的にバランスをとったつもりです。
本書をきっかけに、さらに多くの人が統計学を学び、「新たに何をするか考えて決める仕事」をする力を手にしていただければ幸いです。
