マリさん なるほど、納得しました!
堀口先生 では、次に、こんな問題を出してみましょう。先ほど3×4を、3個のリンゴが4皿、と解釈されましたが、同様に考えると、(-2)×3っていくつになると解釈できそうですか?
マリさん えっと、-2が3個あるから、-6ですか?
堀口先生 はい。その通り!じゃ、3×(-2)は?
マリさん あれ?3が-2個分って……?よくわからなくなりますね。
堀口先生 ですよね。でも、かけ算って順番が逆になっても答えは一緒ですよね。
ということは、先ほどと同じ問題になります。3×(-2)=(-2)×3なので、答えが同じ-6にならないとおかしいですね。3がマイナス2個分と考えると混乱しますが、答えは-6とならざるを得ないわけです。一度そのような法則やルールを決めたら、そのルールに従うように演算の答えも考えていく必要があるんですね。
マリさん なるほど。数学が論理って言われている理由が理解できる気がします。
マイナス●個がわからないなら
数値線上で考えてみよう!
堀口先生 もう少し式を変形してあげると、その式の持つ意味がより深くわかってくることでしょう。3×(-2)についてもう少し説明しますね。-2=(-1)×2ですから、つまり-2は、-1が2個分といえます。よって、3×(-2)=3×(-1)×2=3×2×(-1)と変形できますね。つまり、6×(-1)となるわけです。
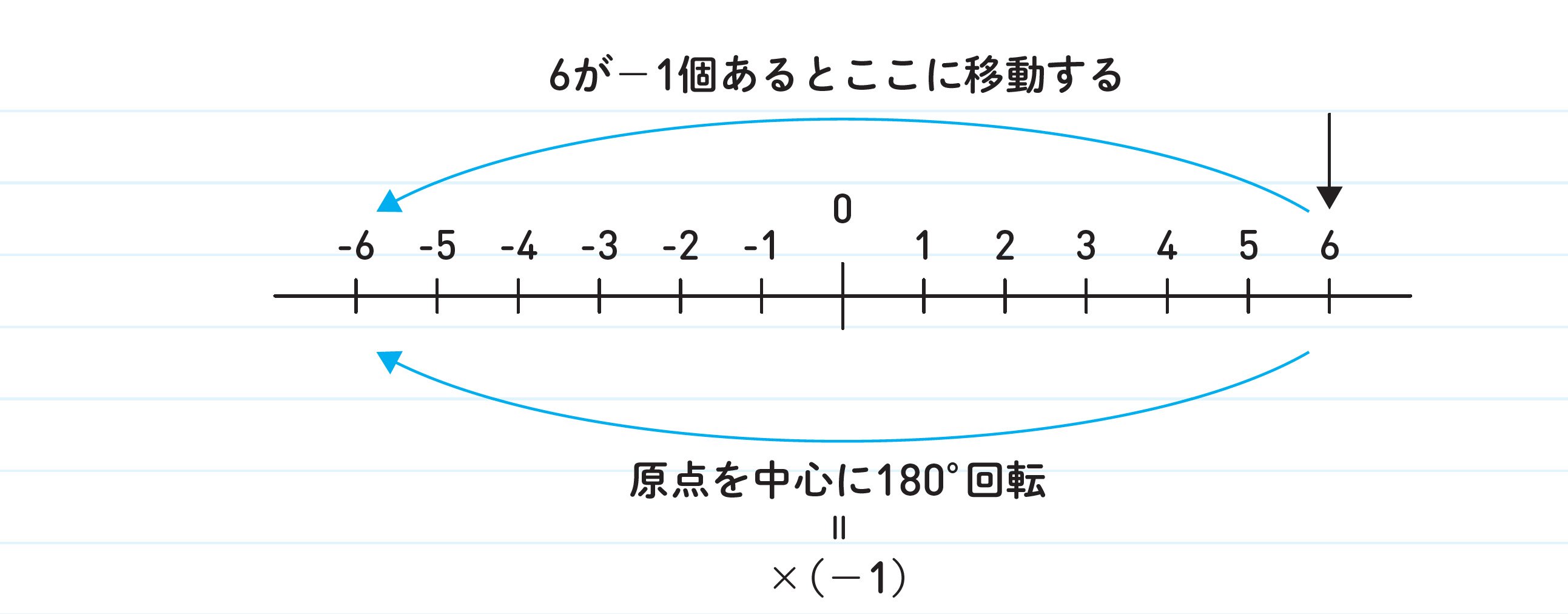
ここで-1をかけるということがどういうことにつながるのかを一緒に考えていきましょう。数直線で考えます。
 同書より 拡大画像表示
同書より 拡大画像表示
堀口先生 6×(-1)は数値線上で6が-6に移動することになります。つまり、6が-1個あるとは、原点を中心に180度回転する、もしくは、原点について対称となる位置にその数を移動させることなんです。つまり、-1個あるとは、回転だったのです!







