「なるほど、駅から徒歩5分の物件は家賃が11万円弱。そして駅に1分近づくごとに、家賃は1500円ずつ高くなっていくのか」
新居を探していた柏木吉基さんは、パソコンの画面を見ながら胸算用をしている。
不動産会社のホームページや物件の検索サイトで比較しているのではない。柏木さんがにらめっこしている画面には、エクセルで自作した点と線だけのシンプルなグラフが映し出されている。それを見て、マンションの家賃を自ら“予測”しているのだ。
柏木さんは日産自動車に勤めるサラリーマン。不動産業の経験があるわけではない。
ただ、サラリーマンの他に、じつはもう一つ別の顔を持っている。それが“統計学の使い手”という顔だ。その実力は統計学をテーマにした著書(「統計を学ぶためのお薦め本」参照)があるほど。そんな“使い手”の手にかかれば、不動産のプロでなくとも駅からの距離で家賃の見通しが立てられてしまうのだ。
では、一体どんなグラフを見て新居を探していたのか。
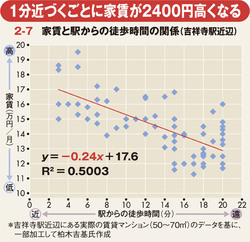
それが図2‐7だ。「住みたい街ランキング」で毎回上位に名を連ねる東京・吉祥寺。その駅近辺にある実際の賃貸マンション(50~70平方メートル)のデータを基に再現したものだ。
なぜ駅からの距離によって家賃を“予測”できたのか。その秘密は、統計分析の中でも「回帰分析」といわれる手法にある。回帰分析とは、二つのデータの関連性を数式で表すことで、分析や予測を可能にする手法だ。
この分析手法を使うと、「駅からの徒歩時間」によって「家賃」がいくら変わるのかという関係性を、y=-0.24x+17.6といった直線の数式に置き換えることができるのだ。ご覧の通り、中学校1年生で習った記憶があるだろう、シンプルな一次方程式。xに徒歩時間を入れると、yの家賃が出てくるというわけだ。
駅からの徒歩時間が増える、つまり遠くなると家賃が安くなっていくので、右肩下がりの直線になっている。そして、直線の傾きから駅に1分近づくごとに、家賃が2400円ずつ高くなることもわかる。
また、図2‐7内にある「R2」は決定係数とも呼ばれ、二つのデータの相関関係を図内の直線が、どれくらいの精度で表せているかを示す数値だ。一般に0.5以上あれば十分といわれる。
この分析方法を応用すれば、自分が持っているクルマが3年後にいくらで中古車買取業者に売れるか、なんてことも“予測”できてしまう。その場合、クルマの買取価格と、買ってからの経過年数や走行距離の相関関係から回帰分析をすれば、同様のグラフができるはずだ。