【思考力チェック！】ある会議で、参加者全員が他の全員に向かって「あなたたちは全員嘘つきだ」と言った。この会議に正直者は何人出席している？

1つずつ、可能性を消していく

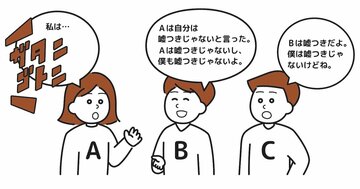
　参加者全員が、他の全員に向かって「あなたたちは全員嘘つきだ」と言っている。
　問題文からわかる情報は、これのみ。
　ここから、真実を探っていかなくてはいけません。

　手がかりが少なすぎる問題ですが、確実に言えることが1つだけあります。

「参加者全員が嘘つき」という可能性はありません。

　もし参加者全員が嘘つきだとすると、「あなたたちは全員嘘つきだ」という発言は真実を述べていることになるからです。
　嘘つきが真実を話していることになるため、矛盾します。

　まず1つ、可能性が排除されました。
　まあ、「みんな嘘つきって言ってるから、正解はみんな嘘つき！」という問題だったら、いくらなんでも簡単すぎますからね。
　そんなにうまくはいかないものです……。

もし正直者が1人なら？

　少なくとも1人は正直者がいるとわかりましたが、その人数に関するヒントはありません。
　それなら、

「もし正直者が～人いたら？」と仮定して、とりあえず考えを進めてみましょう。

　ではまず、もし正直者が1人いたとしたら。
　この1人を、仮にAとしましょう。

　A以外の人たちは、全員嘘つきです。
　その嘘つきの人たちが「あなたたちは全員嘘つきだ」と言っている。
　でも実際には、Aという正直者が1人いる。
　よって嘘つきの人たちの発言は、ちゃんと「嘘」になっています。

　一方で、正直者であるAも「あなたたちは全員嘘つきだ」と言っている。
　実際にA以外は全員嘘つきなので、この発言にも問題はないですね。

「正直者が1人」というパターンは、どうやらありえそうです。

では、正直者が2人なら？

　次に考えるのは、もし正直者が2人いたとしたら。
　この2人を、それぞれA,Bとしましょう。

　A,B以外の人たちは、全員嘘つきです。
　その嘘つきの人たちが「あなたたちは全員嘘つきだ」と言っている。
　でも実際にはA, Bという正直者が2人いるので、嘘つきの人たちの発言はちゃんと「嘘」になっています。

　一方で、正直者であるAが「あなたたちは全員嘘つきだ」と言うと、もう1人いる正直者のBも嘘つきということになります。
　これでは、正直者であるAが嘘をついたことになってしまいますね。
　よって、このパターンは成立しません。

　これは、正直者が3人以上いる場合も同じです。
　自分以外にも正直者がいる場合、正直者の「あなたたちは全員嘘つきだ」の発言は真実ではなくなってしまいます。

　自分以外の全員が嘘つきであるときのみ、正直者は「あなたたちは全員嘘つきだ」と言えます。
　つまり、正直者は1人しか存在できません。

＜正解＞
　正直者は1人だけ

「思考」のまとめ

　こんなに短い問題文でも、ちょっと考えさせられるのが面白いですね。
　ぱっと見では「具体的な人数もわからないし、答えられるわけがない」「考えるだけ無駄」みたいに思ってしまいがちな問題ですが、仮定して考えてみるとちゃんとわかりました。
　思考することをすぐに放棄せず、ちゃんと考えてみることの大切さを教えてくれる良い問題でした。

　ただ、結果としてはたった1人の正直者が、嘘つきたちに囲まれているということに。壮絶であることには変わりありませんでした……。互いを嘘つきだと罵り合う群衆のなかでも、たった1人真実を叫び続ける。そんな人間になりたいものです。

　・「絶対にわからない！」と感じるものも、じっくり考えてみると、真実が見えてくることがある

（本稿は、『もっと!! 頭のいい人だけが解ける論理的思考問題』から一部抜粋した内容です。書籍では同様の「読むだけで賢くなる問題」を多数紹介しています）