「考える楽しさを教えてくれる、全世代におすすめの一冊」
と話題になっているのが、書籍『もっと頭のいい人だけが解ける論理的思考問題』（野村裕之著、ダイヤモンド社刊）だ。Google、Apple、Microsoftといった超一流企業の採用試験でも出題され、“地頭力”を問う知的トレーニングとして注目される「論理的思考問題」の傑作を紹介している。「家族みんなで楽しんでます」「本を読まないうちの子が夢中になっていた」と全世代から反響を得ている同書から、「状況を整理して考えられる人」だけが解ける問題を紹介しよう。（構成／ダイヤモンド社・石井一穂）
イラスト：ハザマチヒロ
複雑な状況を整理して考えられるか？
「論理的に考える」ことで見抜けるのは、目の前にある真実だけではありません。
次の問題、無数に考えられる可能性を整理できるでしょうか？
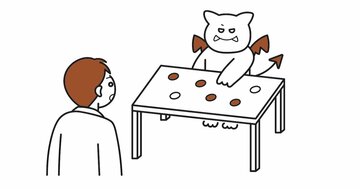
6つの箱が並んでいて、1匹ずつ猫が隠れている。
すべての猫は毎日かならず、1つ隣の箱に移動する。
何日か後に、1箱に4匹が入っていることはありえる？
イラスト：ハザマチヒロ
お。かわいい問題ですね。
1日ごとにとても規則的に移動する猫。
シンプルで簡単なように見える問題ですが、ヒントになりそうな情報が少なすぎて、どう考えたらいいのでしょう？
では、考え方を解説していきます。
予測のつかない猫の動き
1日経つたびに、猫たちは1つ隣の箱にかならず移動する……。
6つの箱にそれぞれ「1～6」の数字をふって、1日目にそれぞれの箱にいる猫を「猫1」「猫2」と呼ぶとしましょう。
つまり、1日目はこんな感じです。
2：猫2
3：猫3
4：猫4
5：猫5
6：猫6
翌日、6匹の猫はそれぞれ1つ隣の箱に移動します。
猫1と猫6は、それぞれ移動できる「隣の箱」が1つしかありませんから、行動が限定されます。
それ以外の4匹は、左右どちらの箱に移動するかわかりません。
たとえば、こんなふうに移動したとしましょう。
2：猫1
3：猫2
4：猫3
5：猫4・猫6
6：猫5
ふむふむ。
では次の日は、たとえばこんなふうに移動したとします。
2：
3：猫1
4：猫2・猫4・猫6
5：猫3・猫5
6：
おお、「4」の箱に3匹が集まりましたね。
こんな具合に考えていけば、やがて1つの箱に4匹の猫が入る日がくるかも？
……はい、大変すぎますね。
考えられるパターンは無数にあります。
ひとつひとつ考えていくのは、ちょっと現実的ではないですね。
猫の動きに「法則」はある？
こんなときこそ、「論理」の出番です。
すべてのパターンを検証せずとも、共通する法則を見つけられれば、論理的に考えることで答えを導けます。
先ほど見たように、猫1匹ずつの動きを追っていくのは現実的ではないので、
猫の動きをいくつかのパターンでまとめられないか考えてみます。
今回、猫が隠れているのは1～6の箱。
つまり1日経つたびに、
・奇数の箱にいるネコは偶数の箱へ
……と、かならず移動するわけです。
1日目、偶数の箱にいる猫は3匹です。
そのすべての猫は2日目に奇数の箱に移動します。
反対に、1日目に奇数にいた3匹の猫は、2日目にはすべて偶数の箱に移動します。
つまり偶数の箱に3匹、奇数の箱に3匹という状況は、何日経っても変わりません。
であるため、どれか1つの箱に4匹が存在する状態はありえません。
1箱に4匹が入ることはない
「思考」のまとめ
猫1匹ずつの行動を読もうとすると困難極まりますが、「猫がどれだけ移動しても、奇数と偶数の配分は変わらない」と見抜けると、先々の動きまで見通せてしまいました。
考えるべき可能性が無数にあるときは、まずいくつかにまとめられないか考えてみる。そうすると複雑な問題もシンプルになって、一気に考えやすくなります。
ただ当然ですが、現実の猫はこんなに聞き分けよくはないので、この作戦は通用しません。でも、そこがまた可愛いんですよね。
POINT
・可能性や選択肢が無数にあるときは、いくつかのパターンにまとめるなどして、共通する「法則」を見つけると考えやすくなる
（本稿は、『もっと!! 頭のいい人だけが解ける論理的思考問題』から抜粋した内容です。書籍では同様の「読むほどに賢くなる問題」を多数紹介しています）
シリーズ累計31万部突破!!
読むほどに賢くなる
最高の知的トレーニング!!
考える力が身につく「最高の知的トレーニング本」
★知識や難しい計算は不要。問われるのは「考える力」のみ!!
★読むほどに賢くなる「思考トレーニング」を58問収録!!
★Google、Apple、Microsoft…一流企業が採用試験で出題した問題も紹介!!
★解けなくても、読むだけで「頭のいい人の考え方」が身につく!!
AIがなんでも教えてくれる時代だからこそ、「ちゃんと考える力」を手に入れよう!!
圧倒的な面白さに、大人も子供も夢中に!!
2024年の年間ベストセラー4位！（ビジネス書部門／トーハン調べ）
28万部突破のシリーズ第1弾はこちら!!
『頭のいい人だけが解ける論理的思考問題』、野村裕之（著）、ダイヤモンド社、2024年3月26日発行、352ページ、ISBN:978-4-478-11904-4（→Amazonで見る）
