リスクを正しく見極めたければ、データの「ばらつき」を数値化する必要がある。では、ばらつきはどのような「手続き」によって定量化できるのだろうか? 今回はファイナンス理論の大前提をなしている「標準偏差」の考え方を『あれか、これか――「本当の値打ち」を見抜くファイナンス理論入門』から紹介していこう。

データのばらつきを数字で表す
――標準偏差「超」入門
リスクとは過去のデータのばらつきであり、ばらつきとは統計学における「標準偏差」である(詳細は前回記事を参照)。
それでは今回は、標準偏差の基本的な考え方をお伝えして行くことにしよう。かなり初歩的な話なので、すでに統計学の知識がある人は前半は読み飛ばしていただいてもかまわない。また、数字が苦手な人は、数式などは読み飛ばしていただいても、大枠は理解できるようになっているのでご安心を。
標準偏差に関係するデータとして、日本人が何よりも親しんでいるのは「学力偏差値」だろう。テストの成績を示す偏差値は、自分の得点が全体の平均点から見てどれくらいの位置にあるのかを指し示している(なお、後述するが偏差値と標準偏差は別の概念なので要注意)。
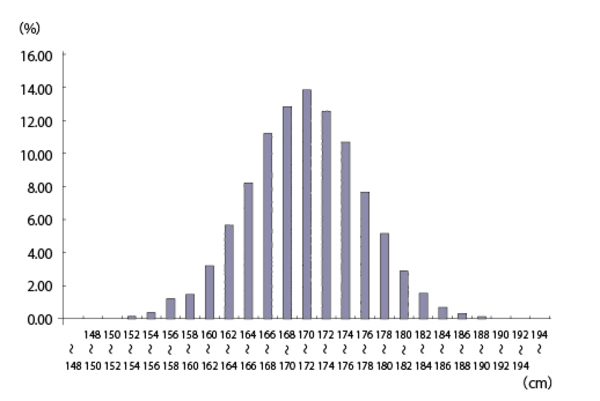
たとえば、ある国の成人男子の平均身長を170センチだとしよう。この場合、大多数の人の身長は170センチの周辺に集まっていて、あとは180センチの人もいれば160センチの人もいるという状態になる。また、190センチ台の人は、たぶん180センチ台の人より少ないだろう。一般に自然界では、母集団のデータを無作為に選ぶと下の図のような釣鐘型のばらつきになることが多い。これを正規分布という。