ファイナンスと統計学はなぜ相性がいいいのか？

すべてのデータがこのようにきれいにばらつくわけではない。たとえば、小学校低学年用の算数のテストを大学生に受けさせれば、ほぼ満点付近に得点が偏ってしまうだろう。

また、人口ピラミッドの形を思い浮かべていただければわかるとおり、年齢ごとの人口分布も正規分布にはならない。そのほか、世代別の所得分布だとか、地域ごとの学力など、社会制度や人為的システムに影響を受けるものは、どうしても釣鐘型のばらつきにはならない。

一方、ダーツとかルーレットのような無作為のゲーム、そしてランダムウォークをする株価の動きなどは、正規分布を描くようになる。

では、実際に標準偏差の出し方を説明していこう。まず、超シンプルな例から。

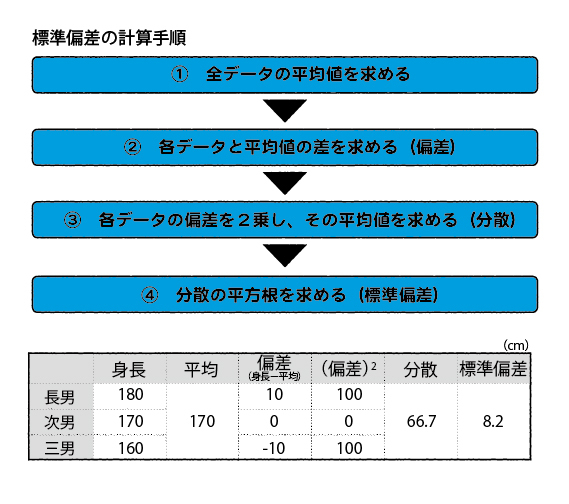
3人兄弟がいる。長男の身長は180、次男は170、三男は160センチだとしよう。3人の平均身長が170センチになることは小学生でもわかる。元のデータと平均値との差を偏差という。長男の偏差は10、次男は0、三男はマイナス10だ。

このとき、平均からどれだけ離れているかだけに注目したい。そこで、それぞれの偏差を2乗する。「偏差の2乗」を比較すれば、長男と三男はともに100（10の2乗）として扱うことができる。つまり、平均より10センチ高いことも、10センチ低いことも同じ事柄として扱えるようになるわけだ。

さらにここで、偏差の2乗の「平均」を計算する。長男100、次男0、三男100の平均は66.7（≒200÷3）だ。偏差の2乗の平均値を分散と呼ぶ。

しかし、この分散を求めるために、先ほど僕たちは「2乗」の操作を加えた。そこで今度は、この66.7という数値に2乗と逆の操作を加える必要がある。要するに、平方根（√）を求めるわけだ。そこで出てくる数字が標準偏差であり、身長の例で言えば8.2（≒66.7の平方根）センチだ。なお、標準偏差は「σ」（小文字のシグマ）の記号で表される。