データの集合が正規分布しているとき、平均値に対して±1σ(1標準偏差)の範囲内に「68.27%」のデータが含まれることがわかっている。これは純粋に統計学の理論上の話だ(詳細な証明はここではしない)。同様に、±2σの範囲には95.45%のデータが含まれ、±3σの範囲には99.73%が含まれる。
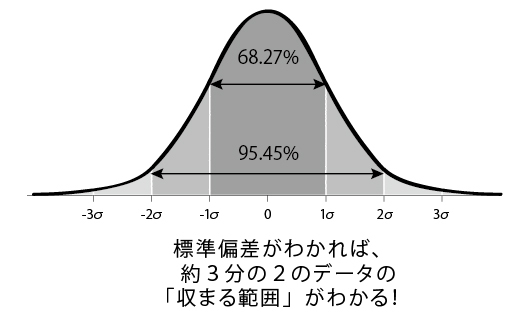
先ほどのテストの得点で考えよう。平均点は77.8点、σ=8.6点だった。つまり理論上は、86~69点の範囲内に68.27%のデータが含まれることになる。実際、得点がこの範囲内にある生徒の数は13人、つまり全体の65%だ。「68.27%」というのはあくまでも理論的な数字であり、サンプルの数が増えれば増えるほど、±1σの範囲に含まれるデータの割合は68.27%に限りなく近づいていく。
同様に、±2σ(17.2=8.6×2)の範囲、つまり95~61点に幅を広げてみると、100%の生徒が含まれる。これもまた95.45%にまずまず近い数字だ。
このクラスの得点の標準偏差が高ければ高いほど、それだけ各生徒の得点にばらつきがあるということだ。高得点をとっている生徒もいれば、ちょっとひどい得点の生徒もいる。
逆に、標準偏差が低くなれば、みんなが同じような点数だったことを意味する。どんぐりの背比べ状態である。
また、万が一、標準偏差が0であれば、ばらつきがゼロだということだから、全員が同じ得点をとったことになる。これはカンニングを疑ったほうがいいだろう。
統計学がデータの予測に使えるのは、標準偏差にこのような性質があるからだ。
たとえば、この学級に転校生がやってきて同じテストを受けたとしよう。標準偏差が8.6のときには、その生徒の得点はほぼ7割(正確には68.27%)の確率で、69~86点くらいの範囲内に収まると予測できる。
しかし、標準偏差が15だった場合、7割のデータが入るレンジが30点分(約69~93点)に一気に広がる。



