今度はみなさんに馴染みのあるテストの成績である。
数学のテストを実施したところ、とある20人のクラスでは下のような得点結果になった。このクラスの得点の標準偏差は?
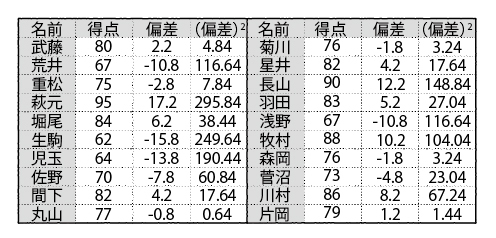
(1)まず平均点は77.8点だ。
(2)この平均点に対して、それぞれの得点がどれくらい離れているか(偏差)を計算する。武藤さんであれば2.2(=80-77.8)、荒井さんであればマイナス10.8(=67-77.8)である。
(3)偏差の正負を無視するために、それぞれの数値を2乗する。武藤さんは4.84、荒井さんは116.64というように、すべてプラスの数値が得られる。これらすべての平均を求めると、分散74.8が得られる。
(4)最後に分散の平方根を求める。このクラスの得点のばらつき度を示す標準偏差σは8.6(=74.8の平方根)となる。
どうだろうか?
それほど難しい計算はないし、エクセルを使えば簡単に割り出すことができるはずだ。ちなみに、俗に言う「偏差値」とは、次のような手続きで計算されている。
(1) 偏差に10をかける
(2) この(1)の数字を標準偏差で割る
(3) この(2)の数字に50を足す
したがって、武藤さんの偏差値は52.6(=2.2×10÷8.6+50)、荒井さんの偏差値は37.4(=-10.8×10÷8.6+50)である。
ファイナンスと統計学はなぜ相性がいいのか?
さて、標準偏差の求め方はわかった。しかしそもそも、この数字は何を意味しているのだろうか? ここでは統計学の解説が目的ではないので、これについては深く立ち入らないようにしよう。「ファイナンス理論を理解するためには、これだけ知っておけば大丈夫」ということだけをお伝えしておきたい。



