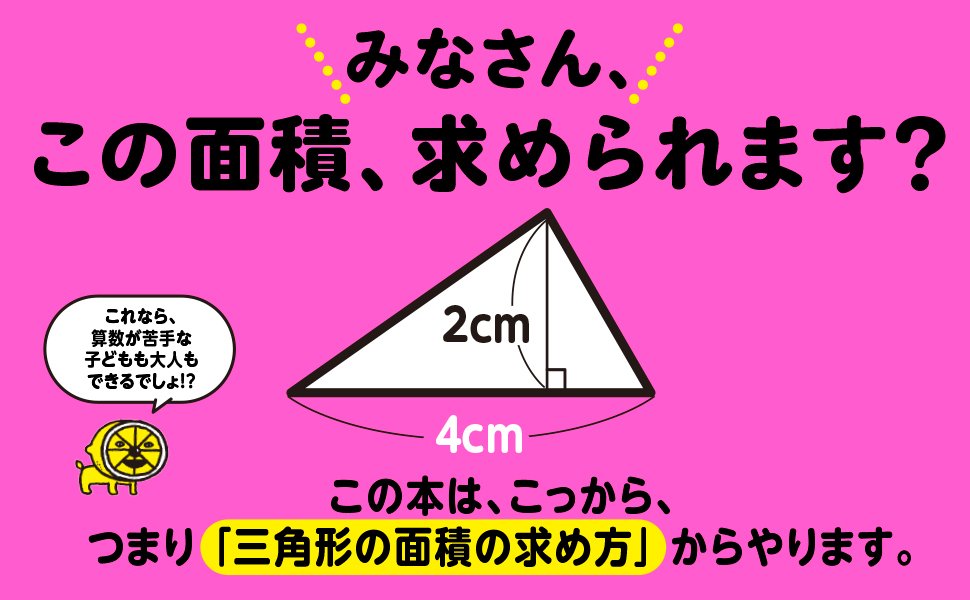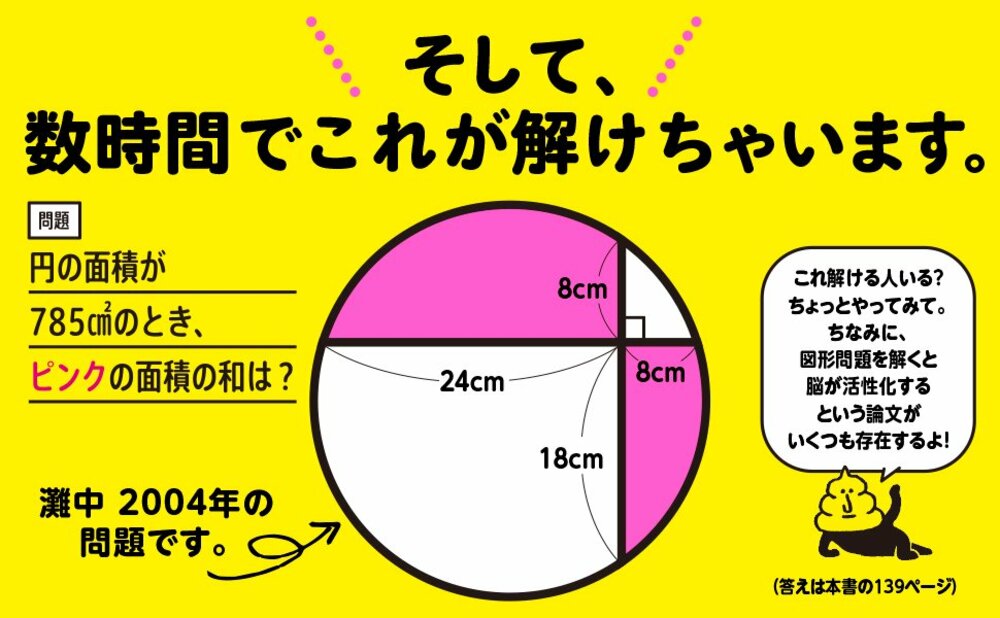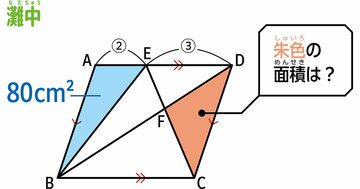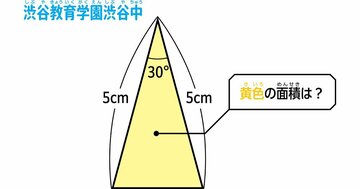
みなさん、いかがですか？
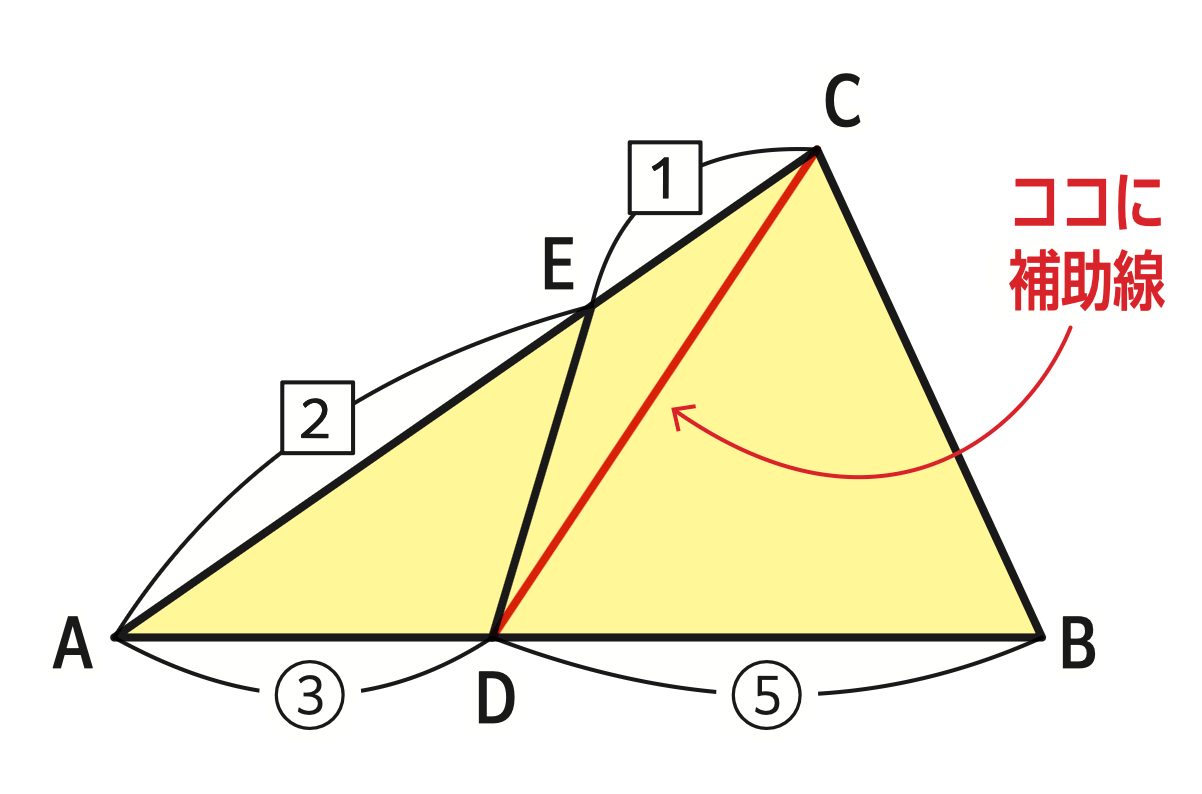
今回はここに補助線を引くんです（上図）。
補助線を引いたらまずは、三角形ACDを見てみましょう。
下の図のように引いた補助線CDで切り離してみるとわかりやすいです。
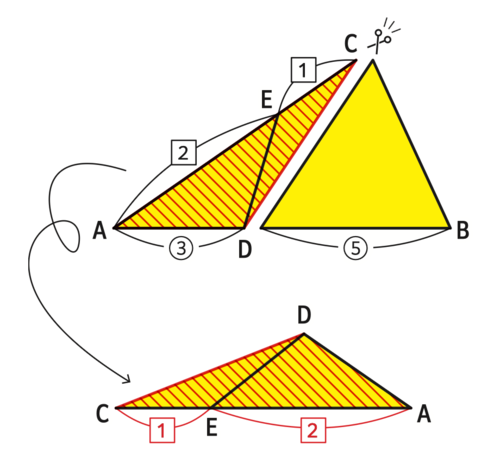
ここで、三角形の辺の長さと面積比の関係を思い出しましょう。
『たった1日で誰でも開成・灘中の算数入試問題が解けちゃう本』（ダイヤモンド社刊より）
この三角形DCEと三角形DEAも高さが同じふたつの三角形なので、
底辺の比、1：2がそのまま面積比になります。
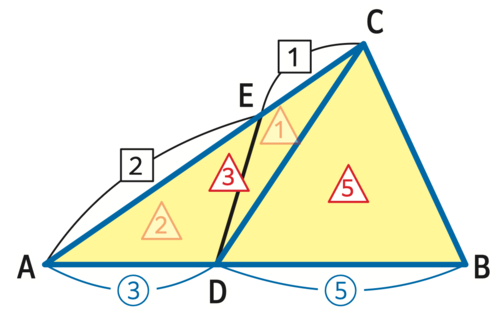
元の三角形に書き込むとこんな感じ（下図）。
さて、三角形ABCに戻りましょう。
三角形CADと三角形CDBも先ほどと同じく、高さの同じ三角形なので、
底辺の比3：5がそのまま面積比になります。
ちなみに、三角形DCE：三角形DEA＝1（△）：2（△）とさっき求めたので、三角形ACDの比は1＋2＝3（△）と表せます。
先ほども説明したとおり、三角形CADと三角形CDBは底辺と同じ3（○）:5（○）になり、
三角形CDBは3（△）×5/3（3分の5）＝5（△）と表せます。
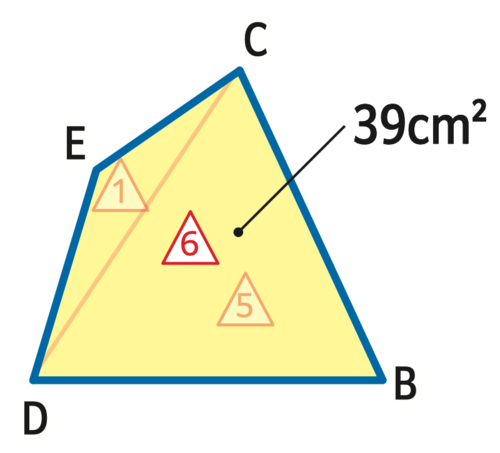
さて、ここで問題文に戻ると、
四角形CEDBが39㎠でした。
三角形DCEが1（△）だったので、四角形CEDBは1＋5で6（△）と表せます。
ここから、以下の式で1（△）が求められます。
そして、三角形DEAは2（△）なので、求めたい三角形は2＋6で8（△）と表されます。
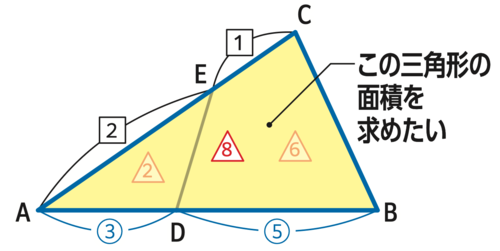
つまり、
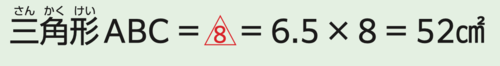
となるので、
答えは、52㎠でした！
みなさん、解けましたか？
manavigate株式会社 取締役／DeNA AIプロダクトマネージャー／株式会社東京産業新聞社 取締役
1994年生まれ。慶應義塾大学総合政策学部卒。
中学受験を経て洛星中学に入学。慶應義塾大学卒業後、新卒で有限会社未来検索ブラジルに入社し、2021年にmanavigate株式会社を立ち上げる。
その後、DeNAのAIプロダクトマネージャー兼AIエンジニアとして、「AIで世の中の働きかたを変える」べく奔走している。
また、自身が運営する算数入試問題を解説するYouTubeチャンネル「まなびスクエア」は、開設から1年で登録者数4万人を突破。
2025年10月の時点で874問を解説し、登録者数は8.41万人に達している。
本書の内容
マンガ「20年前の忘れられない光景」
1時間目
「てっとり早く、頭をよくする方法」と
「友だちを簡単に作る方法」
1時間目-1 てっとり早く、頭をよくする方法
1時間目-2 友だちを簡単に作る方法
2時間目
幸せになるコツと比の話
2時間目-1 幸せになるコツと比の話
3時間目
もう灘中が解けちゃう！
3時間目-1 もう灘中が解けちゃう！
3時間目-2 ○＋×＋90°＝180°
4時間目
パズルみたいな算数問題
4時間目-1 パズルみたいな算数問題
5時間目
いよいよ開成中に挑戦！
5時間目-1 いよいよ開成中に挑戦！
5時間目-2 君たちは天才的な補助線が引けるか？
5時間目-3 ほんとうに灘中が解けちゃうの？
【巻末 袋とじ】
これ解けたら、マジで天才！ いや、神です。
正答率、なんと0％。
『たった1日で誰でも開成・灘中の算数入試問題が解けちゃう本』 菅藤佑太 著
