……念のため3回ほど問題文を読んでみましたが、どうやら間違いないようです。小学生レベルの問題を出題してしまったようですね。
答えは6メートル。それ以外ありえない。絶対に。
でも、「難問」ということは……？
驚愕の答え
えー、先ほど「答えは6メートル以外ありえない」と言いましたが、この問題の答えを知ったとき、私は驚愕しました。
はい……正解は6メートルではありませんでした。
いったい、どういうことでしょうか？
どう考えても答えは6メートルのはずなのに……。
完全に困惑していますが、答えが違う以上、もういちど状況から確認してみましょう。
・それぞれの観察者は1分間ずつカタツムリを観察する
・いずれの観察者が見ている1分間でも、カタツムリはちょうど1メートル進む
この状況で「カタツムリが進める距離」の最大値を考えます。
言い換えると、「観察のされ方を工夫するとカタツムリはどれだけ遠くまで行けるのか？」を考える問題です。
……いっけんすると「6分間ずっと見られていて、1分あたり1メートル進んだなら、どんなに遠くても6メートルまでしか進めないんじゃないの？」と思います。
私もそう思います。なんならいまもちょっと疑ってます。
しかし、この問題が面白いのはここから。
じつはカタツムリは私たちが思っているより遥かに遠くへ行けます。
観察者が6人いるとき
まずはわかりやすいパターンとして、6人の観察者がちょうど1分ずつ交代して観察した場合のカタツムリの動きを考えてみましょう。
・1～2分：観察者Bが見ていて、その間に1メートル進む
・2～3分：観察者Cが見ていて、その間に1メートル進む
・3～4分：観察者Dが見ていて、その間に1メートル進む
・4～5分：観察者Eが見ていて、その間に1メートル進む
・5～6分：観察者Fが見ていて、その間に1メートル進む
……うん、当然こうだと思っていました。
このように6人がリレーのようにバトンタッチしていけば、カタツムリは合計6メートルしか進めません。
観察者は何人いる？
いま、観察者が6人いる場合を考えましたが、これは「6分間、カタツムリはつねに少なくとも1人に観察されていた」という状況を満たす最低人数です。
そう、問題文では、
「観察者は6人」とは書かれていません。
“その姿を、つねに少なくとも1人が見ているようにして、真横から何人かで観察した。”
“それぞれ1分ずつ観察したところ、カタツムリは誰が見ていた1分間においてもちょうど1メートル進んだ。”
と書いてあるので、もちろん観察者は7人以上いてもいいわけです。
「いやいや待ってくれ」
「観察者6人ですら6メートルしか進めなかったんだ」
「なら、観察者が増えればもっと進みにくくなるんじゃないか？」
そう思われるかもしれません。
直感としては正しいです。
ますますカタツムリは最長6メートルしか進めないように思えます。
しかし、観察者が増えることで、カタツムリにとっては大きなチャンスが生まれるのです。
観察時間が「重なっている」としたら？
カギになるのは、観察者たちがそれぞれ観察した「1分間」の重なりです。
問題文には「つねに少なくとも1人が観察」と書かれています。
つまり、同時に2人が見ていても問題ありません。
同時に複数の人がカタツムリを観察している時間帯。
これを利用すると不思議なことが起こります。
簡単な例で考えてみましょう。
たとえばこの問題の状況が、こうだったとします。
直感で答えると、答えは1.5メートルです。
そりゃそうですよね。
1.5分間、少なくとも1人に観察されて、2人ともカタツムリが1分間で1メートルしか進んでいないことを確認しているんですから。
ですが、正しい答えは1.5メートルではありません。
カタツムリは1.5分でどれだけ進める？
観察者B：30秒～1分30秒を観察する（1分間）
このように、30秒間の重なりがある状況を考えてみます。
30秒～1分の間は、2人同時にカタツムリを観察している状態です。
Aは最初から観察し、その30秒後にBも観察しはじめる状況です。
では、このときカタツムリはどう動けば「各観察者が見ていた1分間に1メートル進んだ」という条件を満たしつつ、できるだけ長い距離を移動できるのでしょうか？
結論から言うと、2人が同時に見ている間は休んで、1人しか見ていないときに1メートル進むのです。
これでカタツムリは、
1.5分の間に2メートル移動できます。
カタツムリの猛ダッシュ
文字だけで説明するとわかりづらいので、図にしてみます。
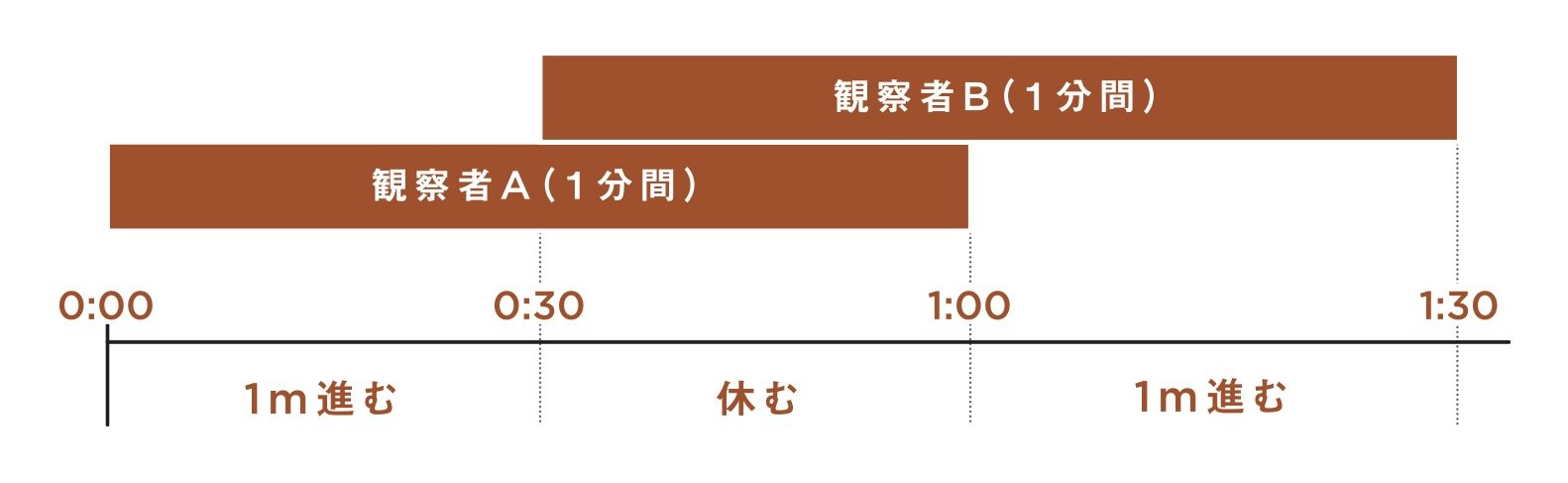
まず、Aだけが観察している最初の30秒間で、カタツムリは1メートル進んでしまいます。
その後、Bも観察をはじめたら、カタツムリは止まって休みます。
こうすると、観察者Aが見ていた1分の間では、カタツムリは1メートル進んだことになります。
一方、開始30秒の時点から見始めた観察者Bからすると、30秒～1分の間は、カタツムリはまったく進みません。
でも大丈夫、この後すぐに挽回します。
開始から1分経つと、Aが観察するのをやめ、カタツムリを見ているのはBのみになります。
この1分～1分30秒の間に、カタツムリは再び動き出して1メートル進みます。
するとBの視点でも、自分が観察した1分間（30秒～1分30秒の間）でカタツムリは1メートル進んだことになります。
さて、この結果どうなったでしょう？
カタツムリは1.5分間で合計2メートル進んでいます。
ところが観察者AもBも、それぞれが見ていた1分間では「1メートル進んだ」と認識しているのです。
このように観察時間を上手く重ねることで、カタツムリは1.5分間で2メートル進めました。
単純計算すれば、1分あたり約1.33メートルのペースにアップしたことになります。
ちょっと不思議ですが、与えられた条件は破っていませんよね。
観察者が増えるといい…？
2人の観察時間が重複すると、カタツムリが進める距離が増えた。
じゃあ3人、4人と増やしていけばもっと伸びるのでは？
ちょっと試してみましょう。
たとえば、先ほどと同じ1.5分間を例に、こんな感じでさらに人数を増やして、観察時間を重複させたとします。
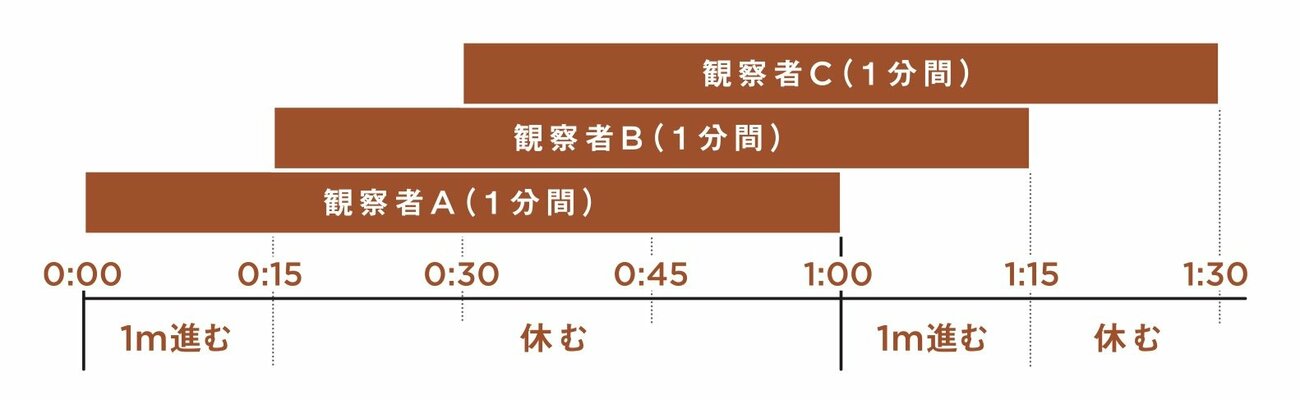
……あれ？ カタツムリが進める距離は2メートルのままですね。
なぜこのようなことが起こるのか？
先ほど確認したように、カタツムリが距離をかせげるのは誰か1人だけが観察しているときです。
複数人が見ている間に1メートル進むと、その全員が見終わるまで、カタツムリは次の移動ができなくなります。
上にある図で言うと、観察者Cが1分間見終わらないと、カタツムリは再び動き出せません。
観察者をやみくもに増やしても効果はなさそうです。
重要なのは「1人しか見ていない時間」
重要なのは、観察している人の数ではなく、
「たった1人しか見ていない時間」を増やすことです。
カタツムリは、「1人だけが見ている時間」が少しでもあれば、その間に距離をかせげます。
ということは、この「1人だけが見ている時間」をたくさん確保すればいいわけです。
時間を長くとるのではなく、「たくさん」確保するのがポイントです。
たとえば、先ほどの「観察者が2人いる」場合、2人の観察時間の重複は「30秒」で考えました。
でもこれが、観察が重複していた時間を仮に「50秒」にしたら、カタツムリは1分10秒の間に2メートル進めます。
図にすると、こんな感じです。
より短い時間で、同じ2メートルの距離を進めました。
このように、観察者の人数を増やした上で、できるだけ2人同時での観察時間を重複させて、「1人だけが見ている時間」をたくさん確保することができれば、カタツムリの移動距離を伸ばせます。
これが、カタツムリが取れる最高の戦略です。
策士カタツムリの戦略
観察者は1分間、カタツムリを見なければいけない。
その上で、2人が同時に観察する時間をできるだけ重複させ、1人が単独で観察している時間をなるべく多く作りたい。
6分間でそれを最大化できるのは、観察者が10人の場合です。
一例ですが、図にするとこうなります。
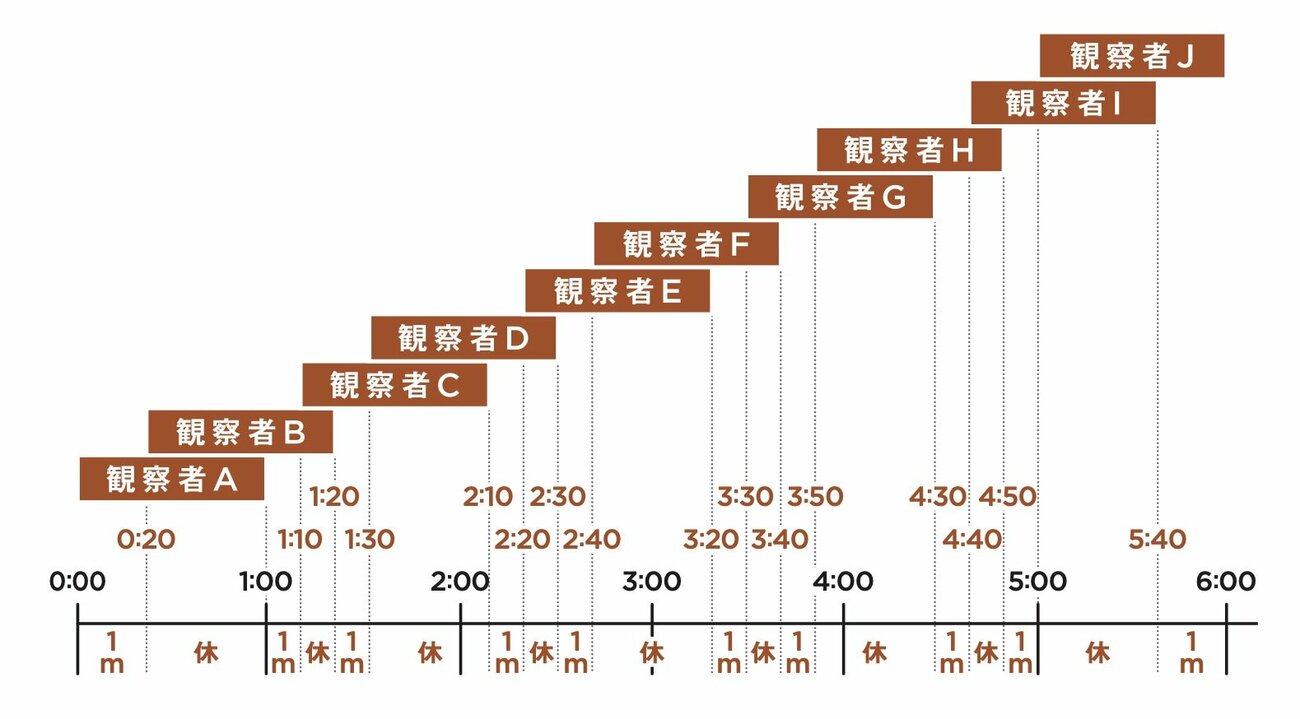
これが、「つねに少なくとも1人に観察されている」という条件を満たしつつ、「1人だけが見ている時間」をできるだけ多くとれる状況です。
観察者を10人以上に増やすことも可能ですが、その場合も、「1人だけが見ている時間」の枠はこれ以上増えません。
まるまる1分間観察できる人をもう1人増やそうとすると、各観察者の間が詰まって、どこかの「1人だけが観察している時間」が消滅するからです。
この状況で、1人しか見ていない時間に急いで1メートル進み、2人が重複して見ている時間はお休みしてまったく動かない。
このような動きをすることで、カタツムリは6分間で最大10メートル進むことができます。
カタツムリは最大10メートル進める
この問題から学べること
「カタツムリは1分に1メートルしか進めない」「観察者は6人しかいない」「カタツムリは一定の速度でのろのろと動く」……みたいなことを問題から勝手に読み取ってしまいましたが、これらは先入観でした。
とはいえ、それらが先入観であることに気づけても、一筋縄ではいかない問題だったと思います。ポイントがあるとすれば、複雑な状況のなかで、「カタツムリは1人に見られている間に1メートルしか進めない」という絶対的な条件をまず見つけだすことでしょうか。そこは変えることができないと気づければ、「それなら、1人だけに見られている時間をたくさんとれたら、距離をかせげるのでは？」と、解決の糸口が見えたかもしれません。……私にはできませんでしたが。
状況を冷静に分析する思考の大切さを教えてくれる問題でした。それにしてもこのカタツムリ、足が速すぎませんかね……？
POINT
・確実に変えられない「絶対的な条件」を確認することで、自分が思い込んでいる「じつは真実ではない部分」が見えてくる
（本稿は、シリーズ最新作『もっと!! 頭のいい人だけが解ける論理的思考問題』から抜粋した内容です。本シリーズでは同様の「読むほどに賢くなる問題」を多数紹介しています）
28万部突破のシリーズ第1弾！
大人も子供もハマる「最高の知的トレーニング」
『頭のいい人だけが解ける論理的思考問題』、野村裕之（著）、ダイヤモンド社、2024年3月26日発行、352ページ、ISBN:9784478119044（→Amazonで見る）
☆2024年の年間ベストセラー4位!!（ビジネス書単行本/トーハン調べ）☆
☆シリーズ累計32万部突破!!☆
☆アジア、欧州を含む世界9カ国で翻訳出版決定!! ☆
☆全人類が夢中の「最高の知的トレーニング」!!☆
全世界の5000問から厳選!!
さらに面白くなったシリーズ最新作！
『もっと!! 頭のいい人だけが解ける論理的思考問題』、野村裕之（著）、ダイヤモンド社、2025年11月12日発行、392ページ、ISBN:9784478123461（→Amazonで見る）
☆売れてます！ 発売たちまち、大重版!!☆
☆発売10日で4.5万部突破!!☆
☆Amazonランキング1位!!（「クイズ・パズル・ゲーム」部門 2025/11/21）☆
