次に戦略に対する利得ですが、お互い「強気」を貫くと一番望まない結果、すなわち離婚になると考えて利得をマイナス100とします。片方が折れて「弱気」になったら負けの利得としてマイナス10、もう一方は勝ちの利得としてプラス10とします。
妻が「弱気」すなわち浮気を問い詰めない、かつ、夫も「弱気」すなわち浮気しないは双方利得なしとします。さらにここに夫が浮気をする確率をp（0≦p≦1）、妻が強気に出る確率をq（0≦q≦1）と設定します。
これで妻の戦略に対する利得が計算できます。図4－12の利得表の4つの場合で、それぞれの利得×確率を合計します。
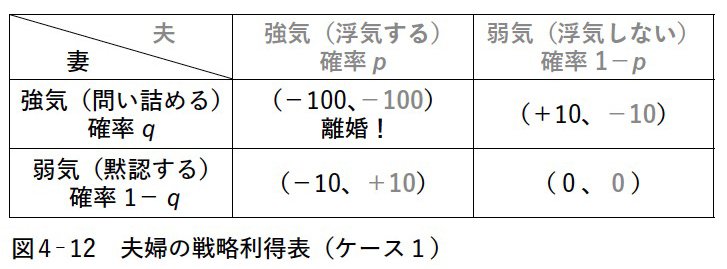同書より転載 拡大画像表示
妻の利得
=－100pq【左上】＋10（1－p）q【右上】－10p（1－q）【左下】＋0（1－p）（1－q）【右下】
=－100pq＋10q－10pq－10p＋10pq
=－100pq＋10q－10p
=q（－100p＋10）－10p
そこで「ー100p＋10」の符号を考えます。これが正であれば、妻の利得はqの増加関数となります。「－100p＋10＞0」より夫が浮気をする確率pが10％未満ならば、q=1、すなわち妻が「強気に出る」を選択すれば妻の利得は最大になります。逆に、夫が浮気をする確率が10％以上ならば、q=0、すなわち「1q=1」となり、妻が「弱気に出る（黙認する）」を選択するときに妻の利得は最大になります。
つまりケース1では、夫が浮気をする確率が10％以上ならば、妻は浮気を問い詰めない（黙認）方がいい、という結論となります。
そもそも妻は夫が浮気をしているかもしれないと疑っていることから夫が浮気をする確率は10％以上だと判断できるでしょう。この場合、妻は浮気を問い詰めない（黙認）方がいい戦略ということになり、離婚は回避される公算が大きくなります。
