写真はイメージです Photo:PIXTA
数学者いわく、「数学嫌い」な人を生み出す要因の1つに、現在の算数や数学の教科書、そして授業のつまらなさがあるという。日本の教育者たちは、その時々の社会や子どもたちの興味を反映した「生きた題材」を扱うべきなのだ――。本稿は、芳沢光雄『数学の苦手が好きに変わるとき』（筑摩書房）の一部を抜粋・編集したものです。
作図文が上達すると
証明文を書く面白味が増す
数学嫌いを生み出す原因のひとつとして、教科書や授業の問題点もあげておきましょう。
たとえば小学校の算数の授業で、「太郎君は1本50円の鉛筆を6本、花子さんは1冊100円のノートを3冊買いました。2人の買い物代金の合計はいくらですか」というような、架空のつまらない文章問題を解いた経験は誰にもあるでしょう。
同じ例を挙げるならば、その時々の社会や子どもたちの興味を反映した「生きた題材」の方がずっと新鮮でワクワク感があります。食材に関しては新鮮で美味しいものが「好き嫌い」に大きく影響するように、数学の学びで用いる題材も同じであることに、もっと配慮したいものです。
それから、中学数学では「作図」を学びますね。作図とは、目盛りのない定規とコンパスだけを用いていろいろな図を描くことですが、昔の教科書と比べて現在は、「作図文」の扱いが軽んじられていることが残念でなりません。具体例で説明しましょう。
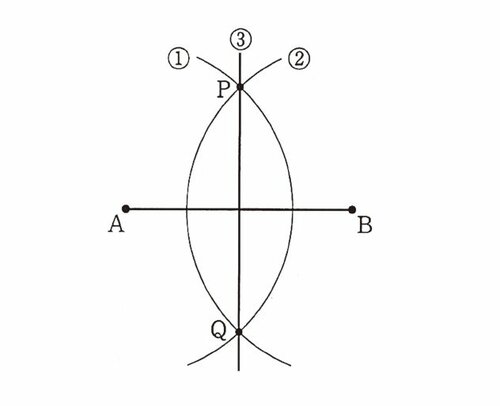
線分ABの垂直2等分線の作図をしましょう。すなわち、ABを2等分する点を通って、ABに垂直に交わる直線を引くことです。以下の（1）から（3）がその作図文です。
（1）点Aを中心として、ABの半分の長さを超える半径をもつ円を描く。
（2）点Bを中心として、（1）と同じ半径の円を描く。
（3）円Aと円Bの交点をP、Qとし、PとQを通る直線を引く。
同書より転載 拡大画像表示
作図文は、その文の通りに図を描くと、求める図が必ず描けるようになっていなくてはなりません。上の例で、（2）の文章を次の（2）′のように変えたとしましょう。
（2）′点Bを中心として、ABの半分の長さを超える半径をもつ円を描く。
この場合、円Aと円Bの交点ができないこともあれば、仮に2つの交点ができても、その交点同士を通る直線を引くと垂線にはなるものの、「二等分」という条件は満たさないことにもなります（実際に試すと面白いですよ）。
上の説明でご理解していただけるとうれしいですが、厳密な論述力を鍛える上で、作図文の学びはとても有効なものなのです。私自身も、作図文によって証明文の書き方が鍛えられたと振り返ります。
