いまからちょうど20年前になる。『週刊東洋経済』で「GNP(国民総生産)が世界一になる日」という特集が組まれたことがあった。
あれから20年、ニッポンは1位になるどころか、GDP(国内総生産)で中国に抜かれて3位に転落した(GNPやGDPの違いは、内閣府の「基礎から分かる国民経済計算」を参照)。そこへ今回の巨大地震である。
筆者の住む栃木県もいまだに余震が続いており、相応に被害が大きい。筆者にできることといえば、義捐金(義援金は代用表記)の振り込みと、買いだめ自粛くらい。
先日は、空から微粒子が降り注ぎ、「放射能だ!」と大騒ぎになった。なんのことはない。スギ花粉である。
みなが神経質になっている中で、震災復興も緒に就いたばかり。世界経済から見れば、ニッポン経済は最後尾からの再スタートである。2位とか3位というのは、政府統計のアヤなのだと考えたほうがいいようだ。
ただし、統計数値の正確性は、きちんと理解しておいたほうがいいだろう。例えば、2011年2月に内閣府が公表した「四半期別GDP速報」を見ると、次の記述がある。

上記の「▲0.3%」は四半期ベースであり、それを年間ベースに引き直したものが「年率▲1.1%」になる、という意味である。その後、2011年3月に内閣府が公表した改定値(2次速報値)は、四半期ベースは同じ「▲0.3%」でありながら、年間ベースは「▲1.3%」へと下方修正されている。
これらのうち、年間ベースの「▲1.1%」や「▲1.3%」は、どのように計算されるのか、ご存じだろうか。まさか、四半期ベースの▲0.3%を4倍すれば、年率▲1.1%や▲1.3%に換算できる(近似する)、と答える人はいないだろう。
小学生でもそのような単純な掛け算で、年率換算できるとは考えていない。私立の小学校では、4年生ですでに「等差数列」を習っているほどのレベルなのである。
経済成長率は単純には計算できない
基本となる「複利計算」の考えかた
四半期の成長率を「 t 」とすると、年率換算の成長率「 C 」は次の式によって計算するのが正しい。
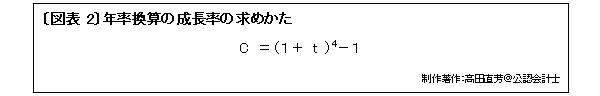
四半期ベースの成長率が▲0.3%であったということは、前期のGDPに比べて当期は0.997倍(=1-0.003)であったことを意味する。この成長率が次の四半期も続くと仮定すると、半年後のGDPは「0.997×0.997=0.997の2乗」、さらに次の四半期は「0.997の3乗」、1年後は「0.997の4乗=0.988」になる。
この「0.988」から「1」をマイナスすると「▲0.012=▲1.2%」になり、これが年間ベースの成長率となる。〔図表 2〕は、以上の説明を1行の式で表わしたものだ。