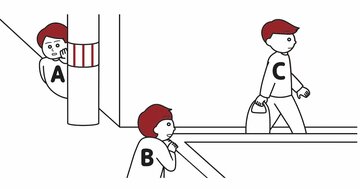
手を挙げた人数が0人のとき、自分は青。
手を挙げた人数が2人のとき、 他に赤がいたら自分は青、 いなかったら自分は赤。
手を挙げた人数が3人のとき、 他が「赤」「青」なら自分は赤。他が「赤」「赤」で その2人が正解を宣言したら自分は青。 他が「赤」「赤」で誰も発言しなければ自分は赤と、特定できる。
論理的思考問題のなかでも頻出の「監禁からの脱出」タイプの問題です。
はじめにお伝えしておきます。
俯瞰思考の問題、ここから一気に難易度が跳ね上がります。
困ったらとりあえずやること
ルールが多く、条件も多い複雑な問題です。
そのうえ、ヒントになりそうな情報も少なそう。
こういう複雑な問題こそ、まずは「パターンの洗い出し」です。
A,B,Cの3人に対して、マークの色は「赤と青」の2つだけ。
起こりうる可能性は以下の8パターンです。
A赤 B赤 C青
A赤 B青 C赤
A青 B赤 C赤
A赤 B青 C青
A青 B赤 C青
A青 B青 C赤
A青 B青 C青
さて、ルールには「もし赤いマークが貼られている人が見えたら手を挙げる」とあります。
これも表に落とし込んでみましょう。
それぞれのパターンのとき、手を挙げる人に★をつけてみます。
A赤★ B赤★ C青★ →手を挙げた人数=3人
A赤★ B青★ C赤★ →手を挙げた人数=3人
A青★ B赤★ C赤★ →手を挙げた人数=3人
A赤 B青★ C青★ →手を挙げた人数=2人
A青★ B赤 C青★ →手を挙げた人数=2人
A青★ B青★ C赤 →手を挙げた人数=2人
A青 B青 C青 →手を挙げた人数=0人
少しずつ糸口が見えてきた
さて、表を見ると、以下の2つのことがわかります。
・誰も手を挙げなかったときは全員「青」のマーク
「手を挙げた人数」がとっかかりになりそうな気がしてきました。
解決のヒントになるのかわからない情報も、いったん俯瞰してみると糸口が見つかるんですね。
では、手を挙げた人数のパターンごとに、状況を詳しく見てみましょう。まずは、手を挙げたのが「2人」のパターン。
A青★ B赤 C青★ →手を挙げた人数=2人
A青★ B青★ C赤 →手を挙げた人数=2人
いずれも「赤のマークは1人だけ」という状況を示しています。
手を挙げたのが2人なら「赤のマークは1人だけ」だと確定しました。
このとき、3人は何を考えるでしょう。
Aの視点で考えてみましょう。
たとえばBとCが青で、その2人が手を挙げている場合、Aは「私が赤だから、2人は手を挙げている」とわかります。
Bが赤、Cが青の場合は、AとCが手を挙げます。
手を挙げないBを見たAは、「私は赤ではない」、つまり自分が青だとわかります。
Bが青、Cが赤の場合も同様です。
Cを見たAとBが手を挙げ、手を挙げないCを見たAは「私は赤ではない」、つまり自分が青だとわかります。
これは、A以外の2人の視点に立っても同じことです。
つまり、手を挙げたのが2人だったとき、3人は、
・自分以外の人に赤のマークがいないなら、自分は赤
だとわかります。
暗雲がたちこめる
「なんだ、手を挙げたのが0人のときも2人のときも自分の色を特定できるなら余裕だ」
そんなふうに楽観的に考えたいところですが……。
ここからが難しくなります。
3人全員が手を挙げた場合、ちょっとややこしいことになるのです。
② A赤★ B青★ C赤★ →手を挙げた人数=3人
③ A青★ B赤★ C赤★ →手を挙げた人数=3人
④ A赤★ B赤★ C赤★ →手を挙げた人数=3人
わかるのは「少なくとも2人は赤のマークである」ということのみ。
たとえばAの視点に立ったとき、自分以外の2人が「1人は赤」「もう1人は青」で、2人とも手を挙げている場合(パターン①と②)は、「自分も赤」だと即座に確定できます。
しかし、
自分以外の2人が「両方とも赤」だった場合、2人はお互いを見て手を挙げている可能性があるため、自分が赤なのか青なのか区別がつきません。
パターン③と④のときです。
どうすればいいのでしょう?
「沈黙」が意味することとは?
ここで活躍するのが、
“3人はきわめて論理的な思考を行う”
というヒントです。
これは、自分以外の2人も、ここまで説明してきたような論理的思考ができるということです。
たとえばパターン③のとき、Aの視点では答えが特定できませんが、B,Cから見たら「自分以外の2人が、1人は赤でもう1人が青」です。
つまり、BとCはすぐに自分の色が赤だとわかります。
BとCが答えられれば、Aは「つまり自分は青だ」とわかります。
一方でパターン④の場合は、BとCから見ても答えが特定できません。
するとどうなるか。
……全員が沈黙します。
ですが、
沈黙によって、「全員が答えを特定できない状態」だということがわかります。
つまり、「全員が赤」だと全員がわかるわけです。
これで、すべてのパターンにおいて、自分の色を特定する方法が見つかりました。
「思考」のまとめ
複雑な問題でしたが、シンプルに考えていくと「パターンを出す」「ひとつずつ検証する」という手順で正解に辿り着けますね。
「全員がわからないことで、答えがわかる」系の問題、個人的にとても好きです。
いっけん八方塞がりに見える状況からでも手がかりを得て突破する感じがこう……心をくすぐりますよね。
・複雑な状況でも、わかっていることを整理していくと選択肢が見えてきて、あらゆる情報がヒントに変わる
(本稿は、『頭のいい人だけが解ける論理的思考問題』から一部抜粋した内容です。)
都内上場企業のWebマーケター。論理的思考問題を紹介する国内有数のブログ「明日は未来だ!」運営者
ブログの最高月間PVは70万超。解説のわかりやすさに定評があり、多くの企業、教育機関、テレビ局などから「ブログの内容を使わせてほしい」と連絡を受ける。29歳までフリーター生活をしていたが、同ブログがきっかけとなり広告代理店に入社。論理的思考問題で培った思考力を駆使してWebマーケティングを展開し、1日のWeb広告収入として当時は前例のなかった粗利1500万円を達成するなど活躍。3年間で個人利益1億円を上げた後、フリーランスとなり、企業のデジタル集客、市場分析、ターゲット設定、広告の制作や運用、セミナー主催など、マーケティング全般を支援する。2023年に現在の会社に入社。Webマーケティングに加えて新規事業開発にも携わりながら、成果を出している。本書が初の著書となる。