イギリスで話題の数学者が伝授！ 誰でも超高速で計算できるワザとは？

「1年は何時間？」もサクッと計算できる！

「1年は何時間か？」と質問されたとしよう。答えはおおざっぱでいい。1年は365日で、1日は24時間なので、365×24だ。暗算で求めるのは難しい。

　でもジコール化すれば簡単に計算できて、

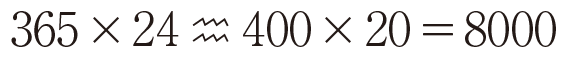
となる。正確な答えの8760と比べてみてほしい。約10％しか違っておらず、ほとんどの場面ではおおよそ合っていると言っていいはずだ。

　大勢の小学生を苦しめる割り算も、ジコールを使えば朝飯前だ。

　5611÷31は？ ジコール化すると6000÷30で、答えは200。やはり正確な答え（181）からそう遠くはない。もっと正確な答えが必要で電卓を使う場合にも、ジコールは役に立つ。電卓に18.1という答えが表示されても、ジコールを使った概算をすれば、電卓が間違えていると分かる（たいていはどこかでうっかりボタンを押し間違えたのだろう）。

ただし、使いどころに注意

　ジコールがけっして正確な答えを出す方法でないことは、口をすっぱくして言っておきたい。とくに2つ目の数字が5以上なら必ず繰り上げるという規則なので、正確な答えからかなりかけ離れてしまうこともある。

　では、どのくらい不正確になることがあるのか？

　例として35.1＋85.2を計算してみよう。整数に丸めて計算すると、120となってほぼ正しい。でもジコールを使うと、40＋90＝130で、これでは10％近くも大きい。しかも130はジコールで100なので、今度は約20％も小さくなってしまう。掛け算では、さらにかけ離れてしまうことがある。

　35×65＝2275でもジコールを使うと40×70＝2800で、2800はジコールで3000だ。30％以上も大きい。これではまずいだろうか？ それはどのくらいの正確さを求めているかによる。

ジコールを使いこなそう

　上の問題で分かったとおり、運が悪いとジコールの答えが正確な答えの2倍や半分になってしまうこともある。そして計算する数が増えれば増えるほど、正解からの外れ具合はどんどん大きくなってしまう。

　そこで、概算の経験が豊富な人ならもっと正確な別の方法を使いたくなるかもしれない。両方の数が切り上げられてしまう場合には、バランスを取るために一方を切り捨てるという方法がよく使われる。たとえば35×65を概算する場合、40×70とするよりも、30×70としたほうが正確だ。もっと正確な概算法を探すのも結構だろう（電卓を使わずに）。

　でも、ここでの目的を忘れないでほしい。いま求めたいのは、おおざっぱに正しい答えだ。多くの場合「おおざっぱ」というのは、「桁数が正しい」、つまり「小数点が正しい位置にある」という意味である。そんなときにはジコールで十分だし、しかも計算がかなり単純になって、ちょっと練習すれば素早く暗算できるという大きなメリットもある。

　ここでさらに重要なポイントを指摘しておこう。矛盾しているように聞こえるかもしれないけれど……。

　ジコールの目的は、すべての計算を単純にして誰でも片付けられるようにすることだ。でも、どんなときにジコールを使うのが適当か、答えをどのように解釈すればいいかは、ある程度の知恵と数に対するかなりの自信がないと分からない。算数が得意であればあるほど、ジコールをうまく使いこなせるのだ。

（本原稿は『世界の猫はざっくり何匹？　頭のいい計算力が身につく「フェルミ推定」超入門』ロブ・イースタウェイ著、水谷淳訳の抜粋です）