2016年の発売直後から大きな話題を呼び、中国・ドイツ・韓国・ブラジル・ロシア・ベトナム・ロシアなど世界各国にも広がった「学び直し本」の圧倒的ロングセラーシリーズ「Big Fat Notebook」の日本版が刊行される。本記事では、全世界700万人が感動した同シリーズの数学編『アメリカの中学生が学んでいる 14歳からの数学』より、本文の一部を抜粋・紹介する。
 Photo: Adobe Stock
Photo: Adobe Stock
第1章 数の種類と数直線
数にはいろいろな種類があって、それぞれ呼び名も違う。
よく使われる数の種類をいくつか紹介しよう。
自然数:分数でもないし、小数部分も持たない、1以上の数。つまり「数を数える」ときに使う数。
例:1, 2, 3, 4, 5…
整数:分数でもないし、小数部分も持たない、すべての数(正の数も負の数も含む)。
例:-4, -3, -2, -1, 0, 1, 2, 3, 4…
有理数:ある整数を別の整数で割ることで表せるすべての数。簡単に言うと、分数(つまり比)で表せるすべての数。
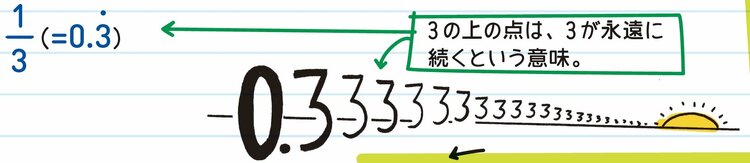
例:1/2(=0.5), 0.25(1/4), -7(=-7/1), 4.12(=412/100), 1/3(=0.33333....)
無理数:分数では表せない数(小数部分が、数字の並びが繰り返されることなく永遠に続く)。
例:3.14159265... , √2
すべての数は小数で表せる。たとえば2は2.000...と書ける。しかしその中でも無理数は、小数で表したときに、数字の並びが繰り返されることなく永遠に続く。
実数:数直線上にあるすべての数。大きい数も小さい数も、正の数も負の数も、小数も分数も含まれる。
例:5, -17, 0.312, 1/2, π, √2 など
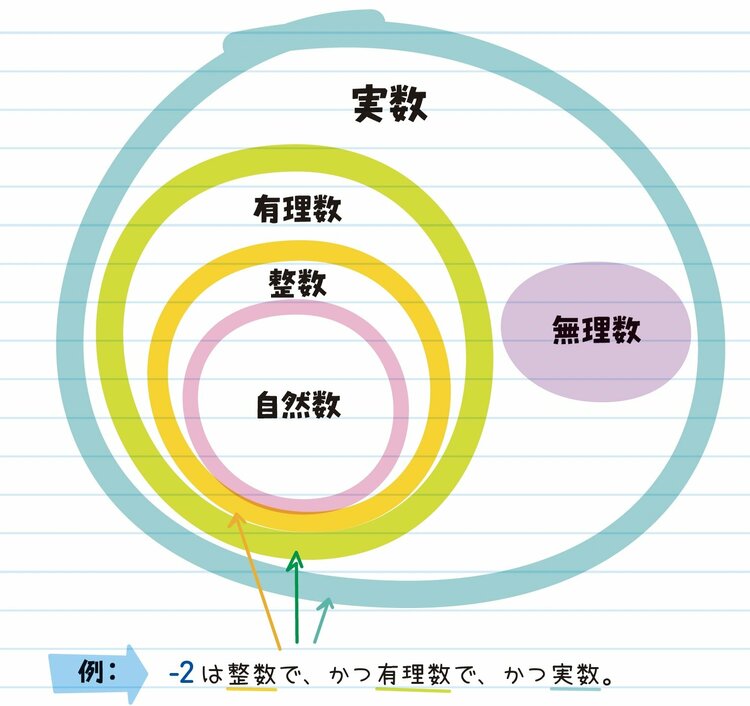
これらの数の種類を図で表すと次のようになる。
ほかの例をいくつか:
・46は自然数で、かつ整数で、かつ有理数で、かつ実数。
・0は整数で、かつ有理数で、かつ実数。
・1/4は有理数で、かつ実数。
・6.675は有理数で、かつ実数(有限小数、つまり数字が途中の桁までしかない小数は、有理数である)。
・√5 = 2.2360679775...は無理数で、かつ実数(数字の並びが繰り返されずに永遠に続く小数は、無理数である)。
数と数直線
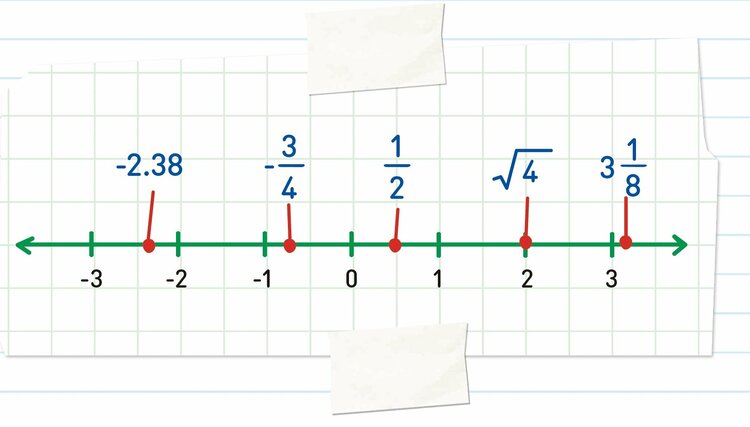
すべての実数は数直線の上に並べることができる。数直線を使うと、数を順番に並べたり、数どうしを比較したりできる。小さい数ほど左側に、大きい数ほど右側に来る。
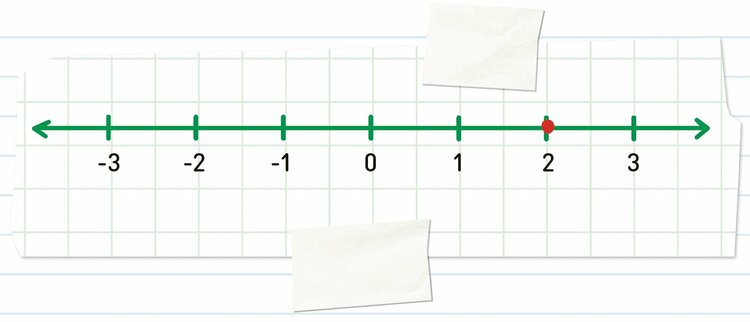
例:2は1よりも大きく、1は0よりも大きいので、右から順番に2, 1, 0となる。
例:同じように、-3は-2よりも小さく、-2は-1よりも小さいので、左から順番に-3, -2, -1となる。
例:数直線の上には整数だけでなく、分数や小数などすべての実数を並べることができる。