2つ目の数字は「サンプルの大きさ」
ただし、対象となるすべての研究で報告された効果の大きさを平均して、全体の効果を算出するのではない。メタアナリシスで注目する2つ目の数字、サンプルの大きさも考慮する。ほかのすべての条件が同じであれば、規模が大きい研究はより多くのデータが含まれており、「真の」効果（全人口における平均的な効果）により近づくと考えられる。言い換えれば、真の効果に関する大規模な研究の最善の推測は、小規模な研究のそれより正確になるだろう。
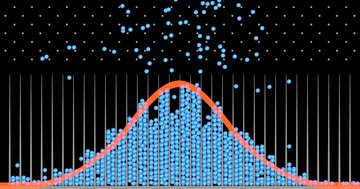
たとえば、男性10人と女性10人を対象とした研究で、並外れて背の低い男性や並外れて背の高い女性など代表的ではないサンプルを偶然選んでしまい、「女性は男性より背が高い」などのような間違った結論を導き出すことは十分に想像できる。一方で、男性1000人と女性1000人を選ぶ場合、並外れた特徴を持つ1000人を偶然、選ぶリスクは、そういう10人を偶然、選ぶよりはるかに低い。
これはほとんどの状況に当てはまる一般的なパターンだ。規模の小さい研究は、より限定的なスナップ写真にすぎず、サンプリング誤差の影響をより受けやすいため、ばらつきが大きくなって、真の効果をより大きな差異で過大評価したり過小評価したりする。
したがってメタアナリシスでは、規模の大きな研究から得られた効果の大きさを、より重視する。
（本稿は、『Science Fictions あなたが知らない科学の真実』の一部を抜粋・編集したものです）
新刊書籍のご案内
スチュアート・リッチー／定価2090円（本体1900円＋税）
［著者］スチュアート・リッチー（Stuart・Richie）
心理学者。キングス・カレッジ・ロンドンの精神医学・心理学・神経科学研究所の講師
2015年に科学的心理学会（アメリカ）の「期待の星（ライジンング・スター）」賞を受賞。『タイムズ』『ワシントン・ポスト』『ワイアード』などに数多く寄稿し、BBCラジオなどの出演もある。X（旧Twitter）は@StuartJRitchie.
［訳者］矢羽野 薫（やはの・かおる）
翻訳者
主な訳書に『人間はどこまで耐えられるのか』（河出書房新社）、『運のいい人の法則』（角川文庫）、『ヤバい統計学』（CCCメディアハウス）、『マイクロソフトでは出会えなかった天職』『ザッポス伝説2.0 ハピネス・ドリブン・カンパニー』（ダイヤモンド社）などがある。
英・米メディア騒然の書、
とうとう日本上陸！
既存の本で知ったウンチクを
得意げに語る人に読ませたい、真実の書。
