睡眠は推論に必要か?
「三段論法」で実験
実験を進めるにあたっては、疑問点を切り分けて、できるだけシンプルにする必要があります。今回の場合、僕たちはまず次のようなクエスチョンを掲げることにしました。
それは、「睡眠は推論に必要か?」です。
推論とは、すでに分かっていることから、未経験の結論を予想することです。僕たちはその中でも、特に推移的推論、平たく言えば三段論法を扱うことにしました。
三段論法とは、前提1:A>B(AはBを上回る)と前提2:B>C(BはCを上回る)という2つの前提を示されたときに、A>C(AはCを上回る)という結論を導き出すことです。
簡単に説明すると、次の通りです。
前提1:アイスクリームは甘い。
前提2:バニラアイスはアイスクリームである。
結論:だから、バニラアイスは甘い。
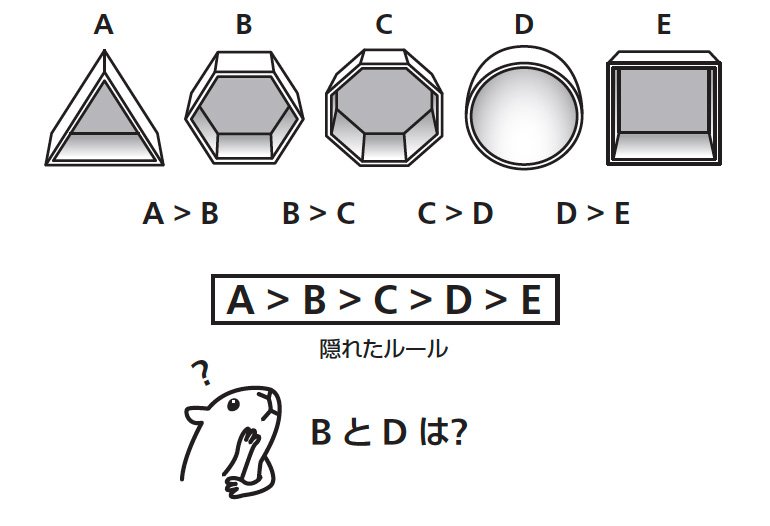
実験では、A、B、C、D、Eの5つの部屋をつくりました。それぞれ、部屋の形と床の模様、壁の模様を変えてあります。
マウスに提示されるのは、このうち2つの部屋の組み合わせです。たとえば、AとBの部屋だけを提示します。スタート地点から歩き出し、マウスは両方の部屋を探索します。そして、Aの部屋に10秒間とどまったときにだけ、砂糖の入ったエサを与えます。マウスに「Aに行けば、報酬がもらえる」ことをインプットするわけです。AとBの関係は、A>Bです。マウスはこの関係を理解し、記憶できます。
同じようにして、BとC、CとD、DとEの組み合わせでもインプットを行います。
つまり「A―B」「B―C」「C―D」「D―E」の組み合わせの部屋を示して、アルファベット順が早いほうに入れば報酬を与えるというトレーニングです。
このトレーニングを14日かけて入念に行ったあと、今度はマウスが初めて見る組み合わせをテストします。それはBとDの組み合わせです。
実験には、A>B>C>D>Eという隠れたルールが存在しています。
 同書より転載 拡大画像表示
同書より転載 拡大画像表示







