【新刊無料公開】
『統計学が最強の学問である［ビジネス編］』第2章 人事のための統計学（6）

ベストセラー『統計学が最強の学問である』『統計学が最強の学問である［実践編］』の著者・西内 啓氏が、ついに待望の新刊『統計学が最強の学問である［ビジネス編］』を発表。ダイヤモンド・オンラインでは、この『ビジネス編』の一部を特別に無料公開。ビジネスパーソンに必要な「統計力」の磨き方について、ヒントをお伝えします。

相関の強い説明変数は「縮約」する

 実際に必要なデータが収集できたらいざ分析に入ろう。基本的な流れは第1章で経営戦略を考えた場合と同様であるが、1つだけ異なるところは、人事のための分析では、企業のときよりも抽象的な要素をさまざまな形で測定するために、縮約という作業がときに必要になるという点である。

 先ほど、スピアマンに言わせれば古典のテストの成績も、音楽のテストの成績も、反応速度についてすら、一般知能ｇという1つの軸で説明できると述べた。これは種々のテスト成績が1つの軸に縮約された、ということである。同様に、80年代の心理学者はそれまでに考案されたさまざまな性格特性をビッグファイブという形で5つの軸に縮約した。このように多数の変数をより少ない数の変数にまとめ直すことを縮約と言う。

 たとえばＳＰＩのように、専門家がきちんと設計した心理検査のためのツール（これを専門用語で測定尺度と呼ぶこともある）であれば、その中に含まれる異なる指標同士が強く相関してしまうということはあまりないはずである。もし万一、そんなことを見つけてしまったら、お付き合いのあるリクルートの営業さんに疑問を呈するべきだ。

 一方で、自分たち自身で新しい質問項目をいくつか作った場合、あるいは、ビッグファイブとＳＰＩの性格検査のように異なる出処の尺度を併用して調査を行なった場合などには要注意である。最低限エクセルの「分析ツール」機能やCORREL関数などでも計算できる相関係数ぐらいは確認したほうがよいだろう。

 たとえば、あなたが専門家が作ったビッグファイブに関する尺度に加え、新たに4つの質問項目を追加して調査を行なったとしよう。それぞれの質問項目に対する答えは全て「まったく当てはまらない」から「たいへんよく当てはまる」まで5段階評価で回答してもらったものとする。その結果、ビッグファイブの得点と、それぞれの項目との間の相関係数を算出すると図表2‐6のようになっていた場合、どう考えたらよいだろうか？

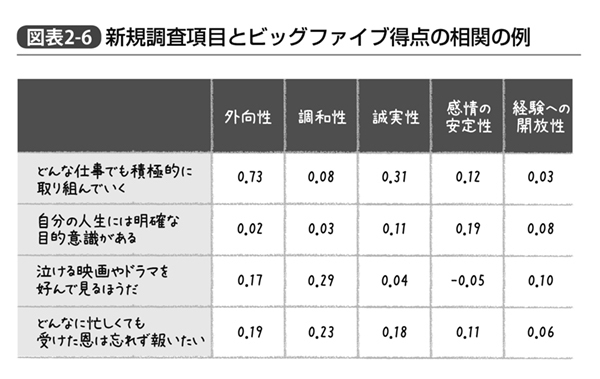
 相関係数がいくつから「大きい」と考えるかという点について数学的に明確な線が引けるわけではないが、慣例として心理検査などでは相関係数が0.3～0.4を上回るか、あるいは逆に-0.3～-0.4を下回る場合には注意する、というのが1つの目安にされることがある。なお相関係数は-1～1までの間の値しかとらず、その間の0という値をとった場合「まったく相関しない」という状態である。

 そのような基準で見てみると、「どんな仕事でも積極的に取り組んでいくかどうか」という姿勢を5段階で回答してもらった結果は、ビッグファイブにおける外向性とかなり相関している。また誠実性との相関にも注意が必要、ということになる。つまり、「外向性が高い人はどんな仕事でも積極的に取り組むと答えがち」なので、このような項目にわざわざ答えてもらわなくてもよいのではないか？ と考えられるのだ。だったらこのような項目は分析から除外し、次回の調査からは外したほうがいい。

 相関の強い説明変数同士を同時に重回帰分析に含めるのは統計学的に望ましいものではなく、せっかく専門家が尺度を作るために行なった配慮を台無しにしてしまうかもしれないのだ。

相関する2項目の得点は合算してもいい

 仕事への積極性以外の、人生の目的意識、泣ける話が好きか、受けた恩に報いようとするかどうか、という調査項目はどうやらビッグファイブの得点とそれほど相関しなかったようだが、これで満足してはいけない。自分たちが作った調査項目同士でも相関が高いものがあるかもしれないからである（図表2‐7）。

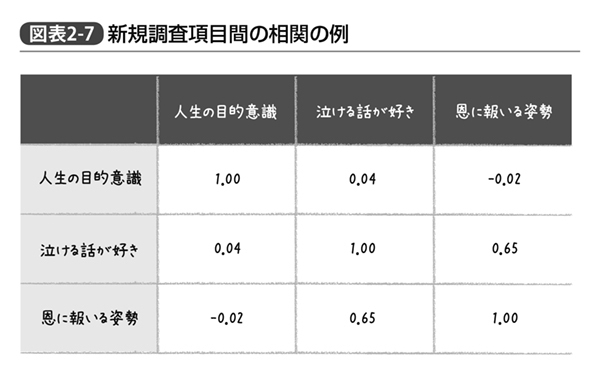
 こちらについても確認してみると、人生の目的意識については他の2項目とほとんど相関していなかったが、残り2つ、「泣ける話が好きかどうか」と、「受けた恩に報いようとするかどうか」は互いに相関しあっていた。こちらについても対処しなければならない。このような場合に考えられる対処方法は大きく分けて2つ。「一方だけを分析に採用するか」あるいは「両者の得点を合算した説明変数を新たに作るか」である。

 前者について、ではどちらを採用すればいいのかという話だが、1つの考え方として「（アウトカムとして採用した）業績との関連性がしっくりくるほう」を採用するというものがある。つまりこの場合で言えば、ただ泣ける映画やドラマを好んで見るような人というだけで仕事ができるとは考えにくい。しかし、そうしたものを好むような人情家であれば、同僚や部下、あるいは顧客と心を通い合わせ、それが結果として業績に繋がるのではないか？ と考えることができる。だとすれば分析すべきは恩に報いる姿勢のほうである。

 一方、両者の得点を合算するという考え方だが、これは「どちらも同じくらい重要だと考えられる」または「それぞれの質問がどうこうというよりも、両者の項目に共通して測定しようとしている『何か』が重要である」と考えられる場合に取るべきやり方である。つまり、今回の例で言えば、泣ける話が好きかや恩に報いる姿勢というよりも、両者の背後にある「人情家度合い」とでも言ったものこそが業績を左右するのではないかとも考えられる。そうすると、いっそ両者の得点を合算することで「人情家度合いスコア」とでもいうものを定義してしまえばいいのだ。

いくつもの項目が相関する場合は「因子分析」を

 なお、ここではビッグファイブのような専門家が作った尺度に加え、ごく少数の質問項目のみを追加で調査に含めたが、実際にはもっと数多くの質問項目のアイディアが生まれ、それぞれ互いに強く相関するもの同士が多数含まれている、という状況も考えられるだろう。

 追加調査項目が20～30といった数を超えると、1つの項目に対していくつもの項目が相関することにもなりうるが、こうした場合何と何をどう足し合わせればよいのか、あるいは何かの項目を分析から除外すべきなのか複雑でよくわからなくなってくる。

 こうした場合に行なわれるのが因子分析である。因子分析の細かい使い方まで説明しだすと本書の意図する範囲を超えるので詳しくは専門書を見ていただくとして、ここでは豊田秀樹著『因子分析入門』（東京図書）に登場する、性格検査の質問項目に対して行なった因子分析の結果を紹介しておこう（図表2‐8）。

 勘の良い方ならもう気づかれたかもしれないが、これらは全てビッグファイブを測定するための質問項目となっている。たとえば他人の気持ちや幸福、子どもに対する関心があり、他人を慰めたり安心させたりするのが得意、というのは調和性である。一方、骨の折れる仕事をやり、時間を無駄にせず計画通り全てが完璧になるまで続けるか、というのは誠実性を示す。

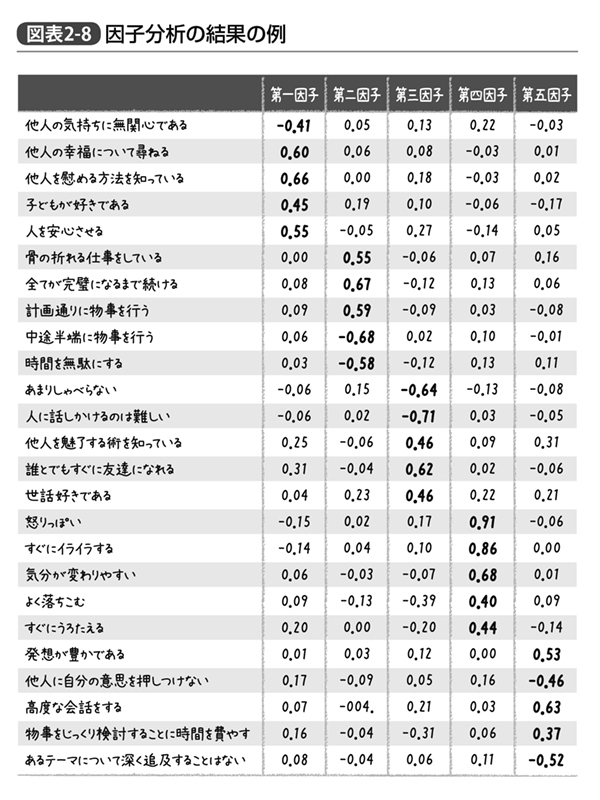
 ここに示された数値は相関係数ではなく因子負荷量と呼ばれるものだが、こちらもやはり-1～1までの範囲を取る。全ての因子について、太字で示した関連する質問項目の因子負荷量はおおよそ0.4以上であり、また逆にそれ以外の（他の因子と関連する）質問項目の因子負荷量は0.4を上回らない（できれば0.3未満）、という状況になれば理想的だが、こちらの結果は概ねその基準を満たしている。

 ここまで整理がつけば同じ因子と関連する項目の得点を足し合わせて『外向性得点』と定義すればよい。専門家が作った質問紙尺度の多くはこのようにキレイに整理されるところまで、質問内容を工夫したり取捨選択して作られたものなのである。

 なお、「他人の気持ちに無関心である」という項目は他の調和性に関する項目と「回答の向きが逆」である。このようなものは逆転項目と呼ばれたりするが、合算するときにそのまま足すのではなく、1～5点でつけられていた元の得点を、1点なら5点、2点なら4点……というように逆転させてから足し合わせる。これは因子分析を使った場合に限らず、前述のような相関の高い2項目を足し合わせる際にも、同様の話である。

 なお、このような作業は大きな注意と労力を必要とするので、調査段階から「できるだけやらなくても大丈夫なように」考えておくというのも1つの選択肢である。つまり、専門家が作った尺度のみを分析に用い、しかも互いに似たようなことを聞いているような複数の尺度を同時に扱わなければいい。

あとは重回帰分析かロジスティック回帰を

 調査した説明変数間の相関性について、ここまでの整理がついていればあとは基本的に第1章と同様である。

 もしアウトカムが売上や粗利の金額、あるいは処理した業務件数といった定量的な数値で示されるものであれば重回帰分析と自動的な変数選択を行なう。すでに述べたように、必要に応じてアウトカムの数値を対数化してもいいだろう。あるいは、もしアウトカムが誰かの評価による「優秀と考えられるか否か」といったように定性的なものであるならば、重回帰分析の代わりにロジスティック回帰を用い、同様に変数選択を行なう。

 なお、前著『統計学が最強の学問である［実践編］』でも書いたように、因子分析で縮約したあと回帰分析を行なうよりは、推定精度の問題などから、構造方程式モデリングなどを使い、一気に変数間の関連性を分析すべきという考え方もある。

 また、細かい話ではあるが、人材の優秀さを「非常に優秀／まあ優秀／ふつう／優秀でない／まったく優秀でない」といった5段階で採点した場合、そのままのアウトカムを順序ロジスティック回帰という手法で「何の説明変数が優秀さのランクに関係しているんだろう？」という分析を行なうこともできるが、私はあまりこのやり方をおすすめしない。

 なぜなら「非常に優秀な人材とそれ以外」を分ける要因と、「ふつう以上の人材とダメな人材」を分ける要因は往々にしてまったく別だからである。同じ優秀な人材を求めるにしても、とにかく非常に優秀な一握りの人材がほしいのか、それよりむしろハズレに当たらないよう注意して全体を底上げしたいのか、どちらがイメージに近いのかよく考えておいたほうがいい。そのうえで、仮に元データが5段階評価だったとしても「非常に優秀か／それ以外か」あるいは「ふつう以上か／未満か」といったように二分するようアウトカムを作り直し、一般的な（二値）ロジスティック回帰を行なったほうがよいだろう。もちろんどちらも知るべき重要な情報だというのであれば、ぜひ両方やってみればよい。

 重回帰分析の結果はすでに前章で説明したので、ロジスティック回帰の分析結果の読み方を学ぶために、図表2‐9のような結果が得られたところを考えてみよう。なお、分析したアウトカムは上司や同僚からの360度評価により得られた「上位5％の優秀な社員と考えられるか否か」という項目であったとする。

 こちらの結果をどう解釈し、またどう活かして利益に繋げるか、次から詳しく述べていこう。