統計の不正を見抜く「ベンフォードの法則」で、米国大統領選を分析するとどうなるだろうか（写真はイメージです） Photo:PIXTA
数学の「奇妙な法則」で読み解く
日本の人口と都知事選の真実
数学の世界には、文系の人にはどうにも理解しがたい「奇妙な法則」が存在します。具体例でお話ししましょう。
日本の市区町村の人口ですが、東京都世田谷区は約90万人、国立市は約7.3万人、檜原村は約2200人、青ヶ島村は178人と、こんな感じでそれぞれの地域の事情に応じて、ばらばらな数字になっています。
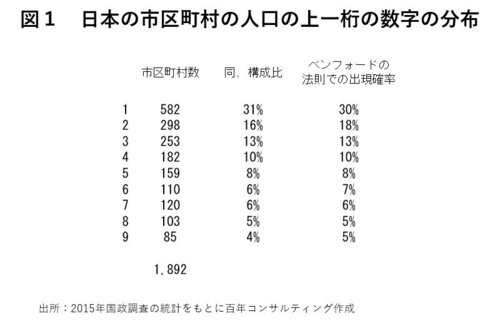
そこでクイズです。この人口の一番上のケタの数字、つまり世田谷区は9、国立市は7、檜原村は2、青ヶ島村は1というように、一番最初の数字だけを取り出してみると、1から9までのどの数字が一番多いでしょうか。
「ランダムに分布する数字であれば、1から9までのどれが多いかはわからないというか、ばらばらに分布するんじゃないのか？」
たぶん、一部の数学者を除いた大半の日本人は、こう予想するのではないでしょうか。
ところが、正解は「1」なのです。
実際に前回の国勢調査の統計表で、全国1892の市区町村（政令指定都市は区単位で計算）を確認をしてみると、人口が「1」から始まる数字の市区町村が582で、全体の31％を占めます。次に多いのが「2」で全体の16％、その次が「3」で13％となっています。
これは「ベンフォードの法則」と言って、「数ケタにわたって分布する統計データでは、上一桁が1～9になる確率は1が一番多く、9が一番少なくなる」というものです。日本の都道府県の人口分布とベンフォードの法則から予想される統計分布を比較すると、非常にぴったりと一致していることがわかります。びっくりしたのではないでしょうか。
