たとえば、ある詐欺師がカモ(その詐欺の被害者)に対して、こんな「勝てば2倍」の賭けを持ちかけるとしよう。「あんたが2個のサイコロを続けて振り、7が出る前に8が出ればオレの勝ち。その逆ならあんたの勝ちだ」。サイコロ遊びをする人ならたいてい、7(ぜんぶで1, 6; 2, 5; 3, 4; 4, 3; 5, 2; 6, 1の6通り)のほうが、8(ぜんぶで2, 6; 3, 5; 4, 4; 5, 3; 6, 2の5通りだけ)よりも少しだけ出やすいと知っている。なので、カモのほうが勝算は高い。
カモがこの最初の少額の賭けで勝つと、詐欺師は2回目の賭けを持ちかける。「こんどは、7の前に6が出ればオレの勝ち、その逆ならあんたの勝ちだ」。合計6になるのは5通り(1, 5; 2, 4; 3, 3; 4, 2; 5, 1)しかないので、今回もやっぱりカモのほうに分がある。またまたカモが勝つと、詐欺師はいよいよ牙を剥く。賭け金を一気に吊り上げ、「あんたが7を2回出す前に6と8を1回ずつ出せばオレの勝ち。その逆ならあんたの勝ちだ」と持ちかける。
一見すると、さっきと同じ賭けを拡張しただけのように思える。ところが、こんどは一転して詐欺師のほうが有利になるというのだから不思議だ。詐欺師の勝率は実に7744分の4255(=54.9%)にもなる。もしも詐欺師が6と8の出る順序を指定していれば、やっぱり詐欺師のほうが不利だっただろう。でも、6と8のどちらが先に出てもよいばかりに、確率が変化したのである。
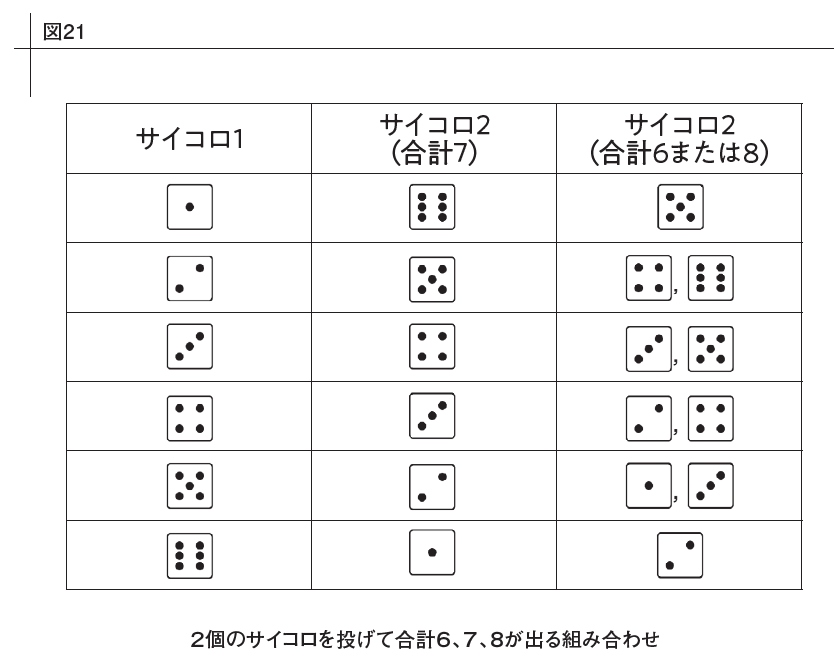
その理由を確かめるため、図21を見てほしい。この図は最初に2個のサイコロを振る時点で起こりうる結果を示したものだ。1個目のサイコロを振って、左の列の数が出た場合、2個目のサイコロを振って合計が7になるために必要な数を中央の列、合計が6か8になるために必要な数を右の列に示してある。この段階では、右の列のほうが圧倒的に確率が高い。中央の列が6/36に対して右の列は10/36だ。いったん6か8が出ると、ふたつ目の数が出る確率は5/36へと戻るけれど、最初の段階での優位が幸いして、全体的には詐欺師が有利なままなのだ。