・もっと効率的に資産を増やせないか?
・会社の財務をもっとうまく管理できないか?
・画期的で新しいアイデアやテクノロジーを生み出して儲けられないか?
不安定さを増す世界で、私たちは好むと好まざるとにかかわらず、日々そんなことを考えざるを得なくなっています。お金で愛や幸せは買えないとはよく言ったものだけれど、お金がなければその先に貧困や満たされない人生が待ち受けているのもまた事実だからです。
16歳でケンブリッジ大学に進んだという逸話を持つアマチュア天才数学者、ヒュー・バーカーは、新著『億万長者だけが知っている教養としての数学』の中で、そんな世知辛い世の中で一際役に立つものこそが「数学」だといいます。「数学を使って儲ける」ためのあらゆる知恵を網羅した同書から、とっておきのトピックを紹介しましょう。(初出:2021年4月18日)
 Photo: Adobe Stock
Photo: Adobe Stock
72の法則
―ー500年使われつづける投資の知恵
ある投資機会やビジネスモデルについて考えるとき、元本が一定の成長率のもとで2倍になるまでの年数を知っておくと便利なことが多い(第一、いつか元本が2倍になるという期待すら持てないなら、もっと儲かる別の投資機会に目を向けたほうがよくないだろうか?)。
72の法則は、その年数を暗算するための簡易的な方法で、少なくともルカ・パチョーリ(1445~1514)が著書『スムマ』で記述した15世紀以来、脈々と受け継がれてきた。
法則はいたってシンプルで、72を成長率(または預金や投資の利率)で割ればよい。そうすれば、初期投資額が2倍になるのにかかる年数がスパッと弾き出される。たとえば、年利9%とすると、72÷9=8なので、8年と算出される。年利9%で元本が2倍になるまでの実際の年数は8.043年なので、確かにこの法則の精度はなかなかのものだ。
ただし、この法則を経験則として使うときは要注意。この法則は概算でしかなく、しかもいちばん値が正確なのは金利が5~10%前後のときだけだ。また、分数の分子として72の代わりに69か70を使うほうが実際には精度が高いということもわかっている。昔から72が使われてきたのは、割り切れる数がたくさんあるからだ。実際、72は、1、2、3、4、6、8、9、12、18、24、36で割り切れる。
数学マニアのみなさんのために言っておくと、分子に69.3を使い、「エックハルト=マクヘイルの二次法則」と呼ばれる次の数式を使うと、計算はいっそう正確になる。
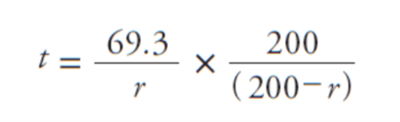
ここで、tは元本が2倍になるまでの年数、rは成長率。第2項は、成長率が高い場合の推定精度を向上させるための補正だ。成長率が高い場合、この補正を行わないと精度が著しく落ちてしまう。
しかし、何世紀も前から多くの資本家や投資家の役に立ってきたという事実が示すとおり、ほとんどの標準的な状況では、基本的な72の法則だけでも完璧に役立つだろう。