統計分析の基本中の基本。それがグラフ化です。
数値データをグラフ化する意義としては、第1に「わかりやすさ」が挙げられます。
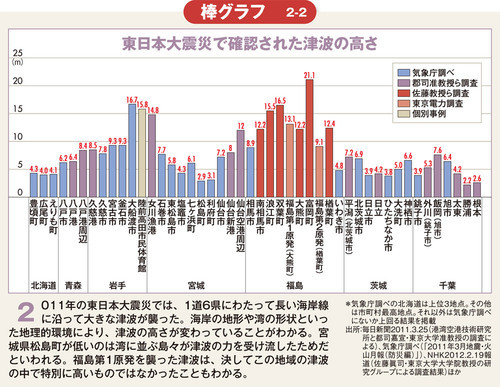
例えば、東日本大震災で起こった個別地点での津波の高さは、棒グラフ(図2‐2参照)で表せば、一目で比較できます。数字を見るより、グラフで視覚化したほうが理解しやすいのは言うまでもありません。大きさ、高さ、時間、金額、人数などの数量を表すとき、素朴だからこそ、最も実感の湧く表現方法が棒グラフです。
さらに、単なる数字の羅列ではなくグラフによって視覚化されることで記憶しやすくなります。「覚えやすさ」がグラフ化の第2の意義です。会議で見たグラフを思い出して電車の中で重要な意思決定をすることだってあります。
また、第3に、見た目にインパクトのある優れたグラフは、「コミュニケーションの手段」にもなります。企画書にグラフが多用されるようになったのもそうした理由からでしょう。壁に張り出された営業成績のグラフも、営業マンの共同行動のきっかけになります。
足して100%となるような構成比(シェア)を表すグラフには、円グラフと帯グラフがあります。
「パイの取り合い」といった言葉があるように、円グラフはシェアを表すのに最も適した表現です。
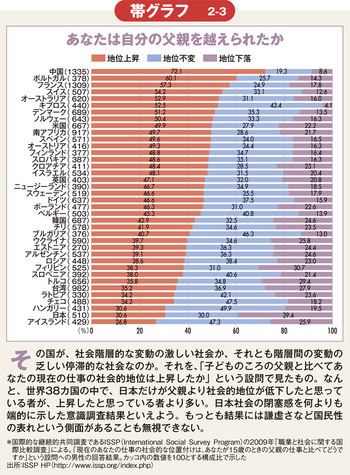
一方、国別比較や時系列変化など、シェアの比較をするときには、円グラフを複数並べることでも可能ですが、微妙な違いを比較するのには向いていません。そういう場合は、帯グラフ(図2‐3参照)が便利です。例えば人口の年齢構成の違いなどを表すには、帯グラフを使用するのが王道です。
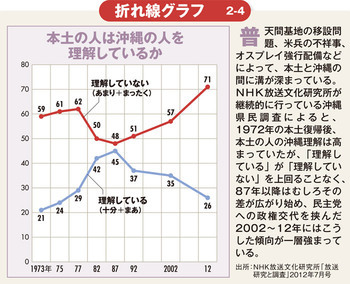
時系列データの表現としては折れ線グラフ(図2‐4参照)が適しています。「この1年で売り上げが2倍になった」といった「量の違い」は、棒グラフがより実感的に表現できますが、「昨年と今年で伸びが2倍になった」といったことを表すには、折れ線グラフのほうが向いています。棒グラフは高さや面積で見分けるグラフ表現であるのに対し、折れ線グラフは角度で見分ける表現だからです。
さらに、点グラフという表現もあります。縦軸と横軸の座標上にデータをプロットしたもので、複数のデータの位置関係や密度などの状態を把握したいときに使うグラフです。