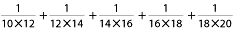中学受験があたり前になった今、受験科目の中で一番気がかりなのは算数ではないでしょうか。「お父さん」に算数を教えていただきたい理由は、「お父さん」こそが、塾の先生や家庭教師よりも、最もお子さんにとって最適な教師となりえるからです。そのためにはまずお父さんが算数の楽しさをご理解いただき、それをお子さんに伝えていただくことが重要です。
当連載では、私(タケウチ)とお父さんのやりとりを通じて、中学受験でよく出てくる算数の問題をわかりやすく解説します。算数の中でも、受験問題でよく出てくる「周期算」「つるかめ算」「食塩水」「平面図形」「計算問題」の5つのジャンルから出題。1ジャンルあたり全3回にわたり、練習問題や過去問題を実際に解いていきたいと思います。
タケウチ:では前回に引き続き、「周期算」のSTEP2です。今回は【例題3】の解説からはじめたいと思います。
【例題】
例題を解いてみよう!
【例題3】
(1)1/7を少数にしたとき、少数第987位の数は何ですか?
(2)7×7×7×…のように7を2006回掛け合わせたとき、一の位の数は何ですか?
------------------------------------------------
式(1)1÷7=0.14285714285…
式(2)987÷6=164…3
式(3)2006÷4=501…2
------------------------------------------------
父:例題3の(1)だけど、もちろん実際に計算するってことはないよね。えっと、どうしようかな……?
タケウチ:式(1)のように実際に計算してみると……。
父:おっ! 小数点以下が142857の繰り返しになってるっ!
タケウチ:あとは簡単ですよね。
父:『1周期の個数』が6個だから、式(2)で987番目までに164周期入って3個余ることが分かる。
| 図1 |
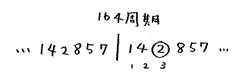 |
タケウチ:そうですね。そして図1のように「周期」の3番目を見れば答えは 2 ということが分かります。
| 図2 |
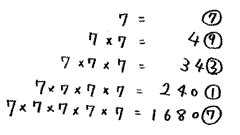 |
父:例題3の(2)も実際にやってみると図2のようになるよね。それで一の位を見ると……。
タケウチ:「周期」は発見できましたか?
父:7931の繰り返しになってるね。